V - Преобразование. Билинейные преобразования. Устойчивость и качество импульсных систем
Рабочие файлы: [Аппроксиматоры] [bi_line_sz.vsm]
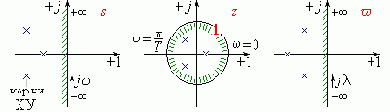
Построим область устойчивости в плоскости комплексной величины z. Воспользуемся методикой D-разбиения и, меняя частоту w
от - Ґ до + Ґ, получим границу z = eTs = e jwT - в виде окружности единичного радиуса, внутрь которой попадает левая полуплоскость комплексной величины s. Следовательно, для устойчивости, все корни-полюсы замкнутой системы F(z)
должны находится внутри этой окружности.
Итак, для описанных с помощью аппарата Z-преобразования импульсных систем, всилу изменившегося вида области устойчивости и периодичности их ЧХ W(e jwT), разработанные для непрерывных систем критери устойчивости (кроме критерия Найквиста и корневого годографа), а так же наиболее эффективные методы коррекции и синтеза (использующие ЛАЧХ & ЛФЧХ) не приемлемы.
Для преодоления этого затруднения используют v-преобразование, которое отражает окружность единичного радиуса на мнимую ось комплексной величины v, с помощью подстановки:
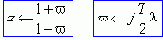
Физически подстановка означает переход к ДУ заменой в РУ элементов чистого запаздывания грубой аппроксимацией - одним фазосдвигающим звеном.
Вторая формула для перехода в область псевдочастот l
получена из соотношения:
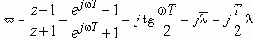
отметим так же, что:
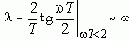
v-Домен и домен псевдочастоты
l используют редко, поскольку для большинства импульсных и цифровых систем частота дискретизации 1/T выбирается в 6...10 раз больше частоты среза. В таком случае выполняется условие wсрT<2, вследствие чего в полосе системы псевдочастота l и частота w практически совпадают. Поэтому обходятся доменом обычных частот, а для переходов используют формулы "Билинейного преобразования":
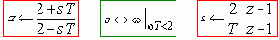
Резюме:
После v-преобразования, используя ПФ W(v) или F(v) можно применять обычные (в основном алгебраические) критерии устойчивости, справедливые для непрерывных систем.
После последующего перехода в область псевдочастот (подстановка
v = jlT/2) вид ПФ W(jlT/2)
и F(jlT/2)
становится пригоден для применения медодов, использующих ЛАЧХ & ЛФЧХ.
Качество импульсной системы может оцениваться построением кривой переходного процесса, что при использовании ПФ F(z) сравнительно легко.
Оценку качества в установившихся режимах удобно выполнять нахождением коэффициентов для разложения ошибки в ряд:
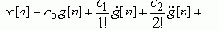
которые являются коэффициентами разложения ПФ Fx(z) в ряд Маклорена по степеням s:
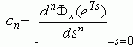
где: z = e Ts.