Условие устойчивости. Типы границы устойчивости

Устойчивость систем зависит от корней характеристического уравнения, поскольку его решение есть сумма экспоненциальных функций:

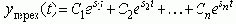
Рассмотрим варианты свободного движения систем от ненулевого начального положения:

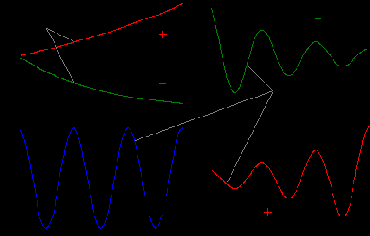
Заметим, что:

C1 e -(a+jb)t

+ C2 e -(a-jb)t

= A e -at sin(bt+j) ,

где: A и j - новые постоянные интегрирования, a - показатель затухания,

b - круговая частота затухающих колебаний.

Таким образом, для затухания переходного процесса и устойчивости линейной системы необходимо и достаточно, чтобы вещественные части корней были отрицательными, те лежали слева от мнимой оси плоскости корней.

Система будет находиться на границе устойчивости при наличии:

нулевого корня,

пары чисто мнимых корней,

бесконечного корня.

Содержание раздела