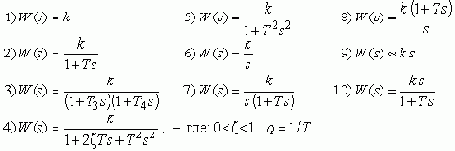Типовые динамические звенья
Рабочие файлы: [Звенья]
Типовые динамические звенья
Совокупность элементарных, универсальных математических функций наиболее часто используемых при построении динамических моделей реальных объектов. Представляют собой ДУ, записанные в особой форме - в виде ПФ связывающих входной и выходной сигналы звеньев. Обычно ПФ записываются не для временного домена, а для домена Лапласа, связывая в этом варианте не сигналы (т.е. не функции времени), а их изображения.
Все типовые динамические звенья
1 Безинерционное звено
2 Апериодическое звено первого порядка
3 Апериодическое звено второго порядка
4 Колебательное звено
5 Консервативное звено
6 Интегрирующее звено
7 Интегрирующее звено с замедлением
8 Изодромное звено
9 Дифференцирующее звено (с минимальным замедлением)
10 Дифференцирующее звено с замедлением
 |
 |
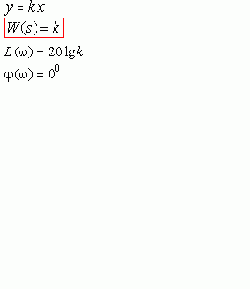 |
Наличие нулевых корней в числителе или знаменателе ПФ типовых звеньев - это признак для разбиения последних на три группы:
Позиционные звенья: 1, 2, 3, 4, 5, - не имеют нулевых корней, и, следовательно, в области низких частот (т.е. в установившемся режиме), имеют коэффициент передачи равный k.
Интегрирующие звенья: 6, 7, 8, - имеют нулевой корень-полюс, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к бесконечности.
Дифференцирующие звенья: 9, 10 - имеют нулевой корень-ноль, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к нулю.