Разложение математического описания модели САР в степенной ряд
Рабочие файлы: [ABCD ®
с1с2с3]
Разложение математического описания модели в степенной ряд
Процедура разложения в степенной ряд системы дифференциальных уравнений САР решенной относительно требуемой координаты. Таким образом результат процедуры – первые коэффициенты разложения (коэффициенты ошибок, или коэффициенты отклика) – получается в результате трансформации либо ABCD-матрицы коэффициентов, либо коэффициентов числителя и знаменателя ПФ.
Известно, что например коэффициенты ошибок связывают коэффициенты разложения входного сигнала g(t) в ряд Тейлора с соответствующими составляющими ошибки x(t) в установившемся режиме движения:
x(t) = c0 g(t) + c1 g'(t) / 1! + c2 g''(t) / 2! + c3 g'''(t) / 3! + ...
Этот факт положен в основу техники разложения математического описания модели в степенной ряд. Идея заключена в том, что библиотека анализа моделирующей программы, за один процедурный шаг, балансирует модель в одном из возможных состояний установившихся режимов движения (неподвижное ненулевое состояние, движение с постоянной скоростью, и т.д.). Далее, измерив значения двух координат (относительно которых требуется выполнить разложение), вычисляет их отношение, находя тем самым соответствующий коэффициент искомого ряда.
В общем виде математическое обоснование техники разложения математического описания модели САР в степенной ряд объемно и опирается на аппарат матричных исчислений (лишь матричное описание позволяет учесть любые возможные взаимосвязи между координатами модели). Поэтому опишем лишь алгоритм, согласно которому функционируют соответствующая процедура библиотеки анализа моделирующих программ:
Пользователь указывает две координаты линейной непрерывной модели: вход и выход, – относительно которых требуется выполнить разложение и активирует соответствующую процедуру анализа.
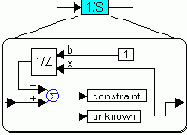
Библиотека анализа замещает все интеграторы модели специальной блок-схемой, изображенной на рисунке справа. К указанному пользователем входу библиотека подключает генератор импульса единичной амплитуды, и подготавливается к измерениям выходной координаты (начиная с этого шага алгоритма допустимо, чтобы программы не использовали графический интерфейс, т.е.
скрывали технические подробности от пользователя).
Далее, библиотека анализа инициирует процесс спец- симуляции модели. На каждом шаге выполняется измерение одного коэффициента разложения (в силу особенностей задающего сигнала значение выходной координаты равно коэффициенту разложения).
Достоинство описанного алгоритма заключается в том, что после упомянутой подстановки, величина шага симуляции моделирующей программы не имеет влияния на результат разложения. Однако процедура балансировки модели требует решения системы линейных алгебраических уравнений, порядок которой равен порядку исследуемой САР.
Если исходной информацией к разложению будут являться не ABCD-матрицы коэффициентов, а коэффициенты числителя и знаменателя ПФ разомкнутой САР, то балансировка модели в установившихся режимах движения может быть упрощена, поскольку итерационному решателю моделирующей программы достаточно прорешивать алгебраическое уравнение лишь первого порядка. Требуемые в этом случае трансформации исходной модели и результат разложения показаны на рисунке.
