Понятие о параметрической функции
Рабочие файлы: [Интеграл Дюамеля] [Интеграл свертки]
[Интеграл свертки]
Очевидно, что реакции САР с var-параметрами на стандартные возмущения 1(t) и d(t) будут зависеть от момента времени поступления сигналов. В связи с этим функцию веса можно изобразить в виде поверхности:
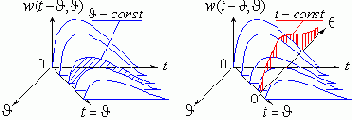
Нормальную весовую функцию w(t-J,J)
при J=const.
Сопряженную весовую функцию w(t-J, J)
при t=const.
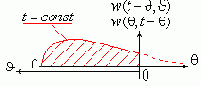
Реверс-смещение сопряженной весовой функции w(q, t-q)
при t=const.
Заметим, что в системах с постоянными параметрами рельеф функций веса цилиндрический и нормальная функция веса совпадает с сопряженной (с реверс-смещением).
Если на систему, со свойственной ей функцией веса w(t-J, J), действует входной сигнал f(t), то элементарная реакция на выходе системы в произвольный момент времени t=J
будет:
dy = w(t-J, J) f(J) dJ
.
Полный сигнал определяется как суперпозиция элементарных реакций:
y = ot т w(t-J, J) f(J) dJ
.
А если использовать реверс смещение q = t-J
(t=const):
y = ot т w(q, t-q) f(t-q) dq
,
то получим интеграл свертки для квазистационарных систем.
Найти функцию веса для систем первого и второго порядков можно аналитически. Для систем высших порядков существуют численные методы.