Метод корневых годографов
Рабочие файлы: [root_locus.vsm]
Метод позволяет подобрать параметры системы по оценке их влияния на общую картину расположения корней замкнутой САР.
Если ПФ замкнутой САР:
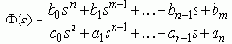
то полюсы и нули (корни) всегда можно вычислить и нанести на комплексную плоскость. Если менять один из параметров системы, (K, ..., Ti, ..., z), то изменения в ПФ F(s) приведут к смещению корней - движению по траекториям, совокупность которых называется корневым годографом. Если менять один параметр, при дискретных значениях другого, то можно оптимально выбрать значения уже 2-х параметров, оценивая семейство корневых годографов. При выборе допустимо пользоваться любой из корневых оценок качества: m, h,
W0.
Наиболее эффективен метод при выборе K. ПФ разомкнутой системы и ХУ запишем в виде:
(*)
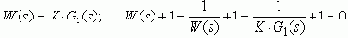
здесь s - не оператор Лапласа или дифференцирования, а любой из корней!!!
Если корни - полюсы и нули известны (q1o, q2o, ..., qmo; q1x, q2x, ..., qnx), то операторную часть ПФ - G1(s) можно представить в виде:
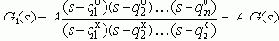
где:
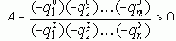
Представим сомножители (s - qi) векторами:
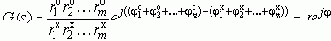
Теперь вновь запишем ХУ:
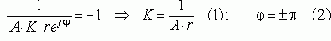
При изменении K от 0 до бесконечности уравнения (1) и (2) определяют правила движения корней:
Если K=0, то корни ХУ (*) совпадают с полюсами W(s), т.к. G(s) должна стремится к бесконечности.
Если K®Ґ, то часть корней ХУ (*) совпадают с нулями W(s), а часть уходит в бесконечность, т.к. G(s)®0 как при совпадении s с нулями, так и при s®Ґ. Наклон асимптот для уходящих в бесконечность корней можно рассчитать по формуле:
(p+2ip) / (n-m), где: i=1,2, ..., n-m.