Критерий устойчивости Найквиста
Рабочие файлы: [fr_ABCD.mcd]
Чтобы система в замкнутом состоянии была устойчивой необходимо и достаточно, чтобы при изменении w от -Ґ
до +Ґ годограф разомкнутой системы W(jw)
(АФХ), поворачиваясь вокруг начала координат по часовой стрелке, охватил точку
(-1,j0) столько раз, сколько корней в правой полуплоскости содержит знаменатель W(jw).
Примечания:
Если корней в правой полуплоскости нет, то годограф W(jw) не должен охватить точку (-1, j0).
Неустойчивая система в разомкнутом состоянии может быть устойчивой в замкнутом состоянии. И наоборот.
Годограф W(jw) всегда начинается на оси "+1". Но при порядке астатизма равном r, по причине устремления W(jw) к
Ґ (при w®0), видимая часть годографа появляется только в квадранте r, отсчитанном по часовой стрелке.
Док-во:
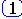
W1(s) = 1+ W(s) = Q(s)/Q(s) + R(s)/Q(s) = D(s)/Q(s) ,
в ней D(s) - характеристический полином, Q(s) пусть не имеет корней в правой полуплоскости (пусть W(s) устойчива).
Рассмотрим угол поворота годографа W1(s). Он равен j = j1(D(jw)) - j2(Q(jw)). Поскольку степень полинома R(s) всегда меньше степени полинома Q(s), то степени полиномов числителя и знаменателя ПФ W1(s) равны. Следовательно при изменении
w от -Ґ до +Ґ:
j1(D(jw))=np
- (по критерию Михайлова), j2(Q(jw))=np
- (по предположению об отсутствии корней в правой полуплоскости у полинома Q(s)). Т.е. j=np-np=0. Другими словами для устойчивости САР в замкнутом состоянии W1(jw)
не должна охватывать начала координат, а функция W(jw) - точку (-1, j0).
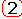
j = j1(D(jw)) - j2(Q(jw)) = n p - [(n - l)
p - l p] = l 2p
,
что и требовалось доказать.