Критерий устойчивости Михайлова

Рабочие файлы: [fr_ABCD.mcd]

Чтобы все корни ХУ:

a0 s n + a1

s n-1 + ... + an-1 s + an

= 0 ,

имели отрицательные вещественные части, необходимо чтобы после подстановки частоты в соответствующий характеристический полном D(s) полное приращение его фазы при изменении w от 0 до

Ґ составляло np/2, где: n

- степень полинома D(s). При этом характеристический полином опишет в комплексной плоскости кривую - "годограф Михайлова".

Док-во: Представим D(s) в виде разложения на линейные множители и выполним подстановку s=jw:

D(jw) = a0

(jw - s1) (jw

- s2) ... (jw - sn) ,

где: s1, s2, ..., sn

- корни ХУ. Скобки идентичны, поэтому рассмотрим одну из них. Возможны четыре основных варианта:

Пусть si=a, - вещественный положительный корень. Тогда годограф соответствующего линейного множителя (jw - a)

при изменении w от 0 до Ґ повернется на угол -p/2.

Пусть si=-a, - вещественный отрицательный корень. Тогда годограф соответствующего линейного множителя (jw + a)

при изменении w от 0 до Ґ повернется на угол p/2.

Пусть si;i+1=a±jb, - сопряженные корни с положительной вещественной частью. Тогда годографы соответствующих линейных множителей (jw - a - jb)(jw - a + jb)

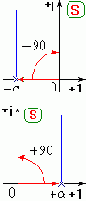
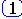
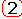
при изменении w от 0 до Ґ повернутся на углы -p/2+g, и -p/2-g. Вектор, соответствующий произведению двух сомножителей, повернется на угол равный -p.

Пусть si;i+1=-a±jb, - сопряженные корни с отрицательной вещественной частью. Тогда годографы соответствующих линейных множителей (jw + a - jb)(jw + a + jb)

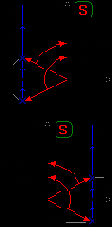
при изменении w от 0 до Ґ повернутся на углы p/2-g, и p/2+g. Вектор, соответствующий произведению двух сомножителей, повернется на угол равный p.

Резюме: Если ХУ имеет l корней с положительной вещественной частью, то угол поворота годографа D(jw) при изменении w от 0 до Ґ составит:

y = - l p/2 + (n - l) p/2 = n

p/2 - l p ,

где: n - порядок ХУ.

Содержание раздела