Каскадные алгебраические петли
Если исходные уравнения модели системы можно представить включенными последовательно блоками, то, очевидно, что программы математического моделирования динамических систем могут однозначно выявить порядок вычислений (составить информационный поток), проверяя готовность аргументов у преобразующих данные функций. Подобный пример был рассмотрен выше.
Однако гораздо чаще в блок-схемах наблюдаются обратные связи (ОС). На рисунке приведена структурная схема апериодического звена первого порядка. Систему уравнений, соответствующую этой блок-схеме, составить легко:
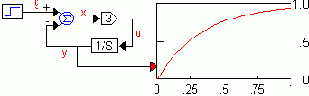
a) g = 1
b) x = g - y
c) u = 3 * x
d) y = oҐ т
u dt
e) график = y
А как составить информационный поток? Для вычисления координаты x надо знать координату y; для вычисления координаты y надо знать координату u; а для вычисления координаты u надо знать координату x. Ситуация кажется тупиковой, но это не так, и только лишь потому, что в контуре (петле) присутствует блок обладающий эффектом памяти (1/S).
Обратимся к функции, которая используется для вычисления интеграла в дискретной форме согласно методу Эйлера с запаздыванием:
y[n] = y[-1] + m=0n-1е
u[m] .
Текущее значение входного сигнала в формуле обозначено индексом n-1, выходное значение индексом n. Легко понять, что на текущем шаге выходное значение дискретного квазианалога интегратора ни как не определено текущим входным значением (связь между текущим входным значением и выходным значением на следующем шаге симуляции не отвергается). Повторим эту мысль в более общей формулировке. На текущем шаге симуляции состояние выходов всех блоков обладающих эффектом памяти не зависит от входного сигнала.
Вернемся к вопросу формирования информационного потока. В свете сказанного становится очевидно, что выходы блоков обладающих эффектом памяти порождают информационные потоки, а входы их замыкают (см. рис.).
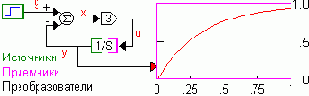
Теперь петля разомкнута, и программа может однозначно сформировать два упорядоченных, зависимых информационных потока для расчета модели:
| 1) g = 1 | 1') y = reg[n-1] + y[-1] |
| 2) x = g - y | 2') график = y |
| 3) u = 3 * x |
|
| reg[n] = reg[n-1] + u |
Если на месте интегратора будет безинерционная функция, то составить информационный поток невозможно - это и есть алгебраическая петля. Алгебраические петли появляются либо при неверном методическом подходе к решению неявных уравнений, либо при ошибочном проектировании цепей обратной связи САР (см. красную цепь на рисунке).
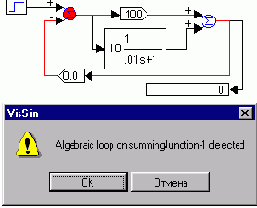
Реальные САР всегда обладают инерционными свойствами. Поэтому более точные математические модели САР обычно не содержат алгебраических петель.
Для решения неявных уравнений программы математического моделирования должны содержать неявные решатели, которые находят решение в процессе итерационного подбора. Наличие подобных решателей в программах – это следующая ступень в их развитии. Программы, преодолевшие этот барьер, как правило, позволяют описывать модели не только направленными, но и ненаправленными графами, т.е. в их библиотеках кроме математических блоков появляются физические элементы: резисторы, транзисторы, двигатели, и пр.