Измерительные алгоритмы идентификации частотных характеристик моделей и систем
Процедуры идентификации ЧХ, основанные исключительно на спектральном или гармоническом анализе результатов измерений входного и выходного сигналов, имеют особую ценность в программах математического моделирования. Они обеспечивают наиболее эффективные и адекватные переходы от абстрактных математических моделей к проектируемым физическим прототипам и обратно, а так же являются одним из не многих инструментов оценки адекватности функционирования самих моделирующих программ в режиме симуляции.
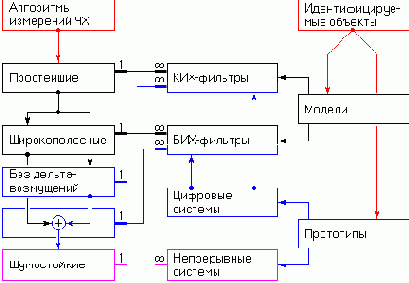
Универсальных алгоритмов измерений ЧХ нет. Существуют три вида ограничений, которые порождают семейства методов измерений ЧХ, которые в той или иной степени могут быть оптимальными для исследования трех классов идентифицируемых линейных объектов (см. рис.). К упомянутым ограничениям относятся:
Невозможность использования дельта-воздействий для объектов с эффектами насыщения.
Затруднения в расширении диапазона частот свыше "трехдекадного барьера".
Большие временные затраты на расширение динамического диапазона ниже уровня шума.
Если на вход системы подать весь спектр частот с единичными амплитудами, то определение частотной ПФ на основе измерительной информации упрощается:
W( jw) = Y( jw)/X( jw) | X( jw)=1
= Y( jw) .
Подобный единичный спектр имеет дельта-функция Дирака
d(t). Реакция же систем на дельта-функцию называется функцией веса w(t), поэтому частотную ПФ можно получить вычислением её Фурье-изображения:
W( jw) = FT { w(t) } ,
или же, для дискретных сигналов:
W [ jkw] = DFT { w[n] } = n=0N-1 еw[n] е -jkwnT .
где: w – частота первой гармоники в спектре сигнала длинной в NT выборок; k – порядковый номер гармоники (независимая переменная); N – число выборок функции веса w[n] (обычно кратно степени двойки); k Ј N/2.
Подобный подход используется в простейших алгоритмах идентификации ЧХ и достаточно легко реализуется в любых математических программах:
document.write('');
программы VisSim (в свойствах блока осциллограф активирован режим вычисления БПФ для осциллограммы)
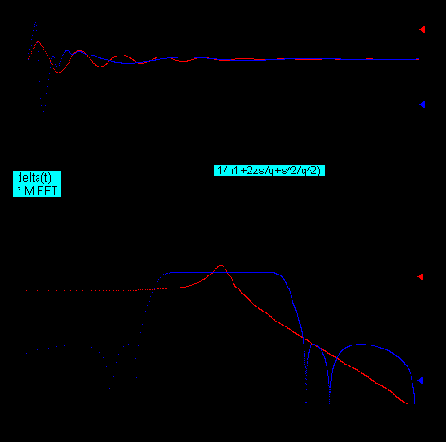
Измерения частотных характеристик выполнены для модели колебательного звена и инверсного фильтра Чебышева десятого порядка, т.е. для двух непрерывных систем с бесконечной импульсной характеристикой (IIR)
Сравнивая приведенные на рисунках ЧХ КИХ и БИХ-фильтров, легко понять суть "трехдекадного барьера" (присущего алгоритмам на базе БПФ), который проявляется при частотном анализе БИХ-фильтров, чьи ЧХ представляются в логарифмическом масштабе по оси частот. Очевидно, что, в этом случае, кратная двойке сетка анализируемых гармоник в выходном массиве процедуры БПФ ограничивает разрешение по частоте в НЧ диапазоне. Увеличение частотного диапазона на декаду требует увеличения времени симуляции в десять раз.
При измерении ЧХ реальных систем использование дельта-функции невозможно. Её замещают либо суперпозицией синусоид, либо белым шумом, либо другим сигналом конечной амплитуды. Основным методом расширения динамического диапазона ниже уровня шума является усреднение результатов повторных измерений. В случае использования алгоритмов измерения ЧХ на базе ДПФ для ослабления эффекта наложения частот используют методику взвешивания массива измерительной информации окнами Бартлета, Хэмминга, с хэннингом, Блэкмана, Хариса и т.д.