ДУ решенное относительно регулируемой величины y(t) - уравнение движения
Рабочие файлы: [САР]
Система ДУ (1) может быть преобразована к одному уравнению путем исключения промежуточных координат (обычно выходную координату выражают через координату задания):
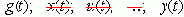
Результатом подобного преобразования является уравнение движения системы:
(4)
D(p) y(t) = R(p)
g(t) - N(p) f(t) ,
где:
D(p) = a0pn + a1pn-1 + ... + an-1p + an
- характеристический полином;
R(p) = D(p) - Q(p) = b0pm + b1pm-1 + ... + bm-1p + bm
- коэффициенты этого полинома определяют влияние задающего воздействия g(t) на регулируемую координату у(t), причем его степень меньше степени характеристического полинома, т.е. m<n;
N(p) = d0pk + d1pk-1 + ... + dk-1p + dk
- коэффициенты полинома определяют влияние помехи f(t) на систему.