Дискретная синусоидальная последовательность
Рабочие файлы: [aliasing.vsm][z_sin2.vsm]
[psd45.vsm] [fft30.vsm] [Свойства W(e jwT)]
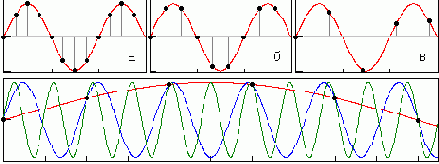
Особые свойства последовательности x[n]:
Функция может быть как периодической - рис. а и б, так и непериодической - рис. в.
Амплитуда образующей непрерывной функции может быть максимальным значением последовательности x[n] - рис. а, и может не является им - рис. б.
Последовательность не изменится, если на вход ключа подавать сигналы с частотами, отличающимися на частоту дискретизации: f ; f + 1f0;
f + 2f0; ...; f + kf0.
Запишем закон изменения синусоидальной последовательности в экспоненциальной форме:
x[n] = a sin [wnT+j] = a e
j[wnT+j] = a e
jj e jwnT = a e
jwnT = a zn
,
тогда выходная величина импульсного фильтра:
y[n] = m=0Ґ еwп[n-m] x[m] = m=0Ґ еwп[m] x[n-m] = m=0Ґ еwп[m] a zn-m = a zn
m=0Ґ еwп[m] z -m = a znW (z) = x[n] W (z).
Таким образом ПФ W(z) при подстановке z = e jwT - есть частотная ПФ. Все остается в силе и для F(e
jwT) и
Fx(e jwT).
Очевидно, что частотные ПФ W(e jwT), F(e jwT)
и Fx(e jwT)
обладают периодическими свойствами (w0 = 2pT -1). Это видно и из нижнего рис., поскольку одну и ту же входную последовательность могут вызывать входные сигналы с разными частотами f + k f0.