Дифференцирование и интегрирование решетчатых функций

Рабочие файлы: [S & 1/S]

Аналогом первой производной для решетчатой функции является либо первая прямая разность:

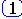
D f [n] = f

[n+1] - f [n],

либо первая обратная разность:

С f [n] = f

[n] - f [n-1].

Аналогами второй производной являются вторые разности. Прямая:

D2 f [n] = D f

[n+1] - D f [n]

= (f [n+2] - f [n+1]) - (f

[n+1] - f [n]) = f [n+2] - 2 f

[n+1] + f [n],

и обратная:

С2 f [n] = С f

[n] - С f [n-1] = f

[n] - 2 f [n-1] + f

[n-2].

По аналогии могут определяться и высшие разности:

Dk f

[n] = n=0kе(-1)nCknf

[n+k-n]

Сk f

[n] = n=0kе(-1)nCknf

[n-n]

где: Ckn = k! / (n!(k-n)!).

Очевидно, что если f [n] определена только для положительных n, то для n=0 все обратные разности

Сk f [n] равны нулю, что позволяет ...

Аналогом интеграла является неполная сумма:

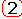
s[n] = m=0n-1е

f [m] = n=1nе

f [n-n],

и полная сумма:

so[n] = s[n] + f

[n].