Цифровые регуляторы
В непрерывных системах широко используются PID-регуляторы, которые представляются идеализированным уравнением:
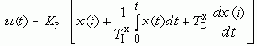
где: KP - коэффициент усиления пропорционального канала; TIx - постоянная времени сопрягающего полюса интегрального канала; TDx - постоянная времени сопрягающего полюса дифференциального канала.
Для малых периодов дискретизации Tц уравнение может быть преобразовано в разностное без существенной потери в точности. Непрерывное интегрирование может быть представлено с помощью метода прямоугольников
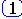
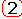
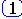
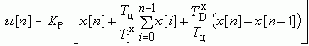
В результате получен нерекуррентный (позиционный) алгоритм управления, который требует сохранения всех предыдущих значений сигнала ошибки
x[i], и в котором каждый раз заново вычисляется управляющий сигнал u[n].
Для реализации программ закона регулирования на ЦВМ более удобным является рекуррентный алгоритм. Он характеризуется тем, что для вычисления текущего значения сигнала u[n] используется его предыдущее значение u[n-1] и поправочный коэффициент, не требующий существенных вычислительных затрат. Определим его:
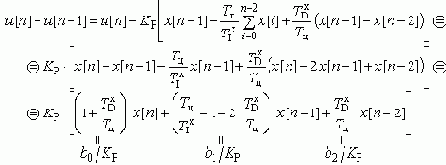
Перенесем u[n-1] в правую часть - получим "скоростной" алгоритм для программной реализации регулятора:
(*)
u[n] = u[n-1] + b0
x[n] + b1 x[n-1] + b2
x[n-2].
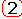
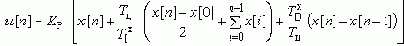
Преобразования, аналогичные выше изложенным, при получении рекуррентного соотношения (*), выявляют отличия только для коэффициента b0:
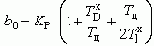
Запишем РУ (*) для изображений в z-домене:
U [z] (1- z -1) = (b0
+ b1 z -1 + b2 z
-1) X [z] ,
и представим его в виде дискретной ПФ:
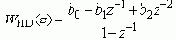
Анализ ее коэффициентов показывает, что:
Для исключения статической ошибки, ПФ должна иметь полюс zx=1.
Если b2 = 0, то получим PI-регулятор.
Если b0 = 0, а b1 = (1 + b2), то получим PD-регулятор.