Архитектура математического ядра моделирующих программ с поточной моделью управления
Какими бы разными ни были моделирующие программы, вариации архитектуры их математических ядер довольно жестко ограничены возможностями компиляторов языков высокого уровня. Очевидно, что математическое ядро должно поддерживать от 100 до нескольких тысяч математических функций. Безусловно, требуется формализация интерфейса настройки и управления математического ядра, поскольку справиться с таким громадным количеством функций, используя их ручной вызов, невозможно.
Возможности современных версий языка Си++ позволяют решить поставленную задачу следующим образом. Пишется полиморфный класс CBlkTemplate с виртуальным методом Calc (см. табл. 1). Его наследуют классы, составляющие библиотеку математических функций. В частности, каждый потомок реализует метод Calc в виде уникальной математической функции. Уточним возможности, которые предоставляет подобная организация библиотеки.
Во первых, от каждого математического класса можно породить любое количество объектов. Это означает, что для обработки повторно встречающихся в модели математических функций будут использованы уникальные экземпляры объектов, каждый из которых будет иметь собственную область памяти для хранения возвращаемых значений Output[k]. В результате не будет наблюдаться "затирание" координат модели.
Во вторых, в силу действующих стандартов для компиляторов языка Си++, объекты порожденные от разных потомков полиморфного класса (CBlkTemplate) будут иметь реализации виртуальной таблицы функций (vtbl) одной размерности. Это означает, что их можно присвоить элементам одного массива MathBlock[i] (см. рис. 3). Что, в свою очередь, открывает возможности для создания автоматизированных процедур обслуживания объектов математического ядра. Так например, процедура исполнения шага симуляции модели в таких программах, как VisSim, Simulink, MBTY может иметь следующий вид:
Листинг 1
for (i=0; i < numBlock; i++) { MathBlock[i]->Calc(); }
Подобных процедур не много, и, в случае реализации математического ядра в виде COM-сервера, они образуют его интерфейсы (см.
табл. 2).
Уделим внимание деталям реализации математического ядра. В табл. 1 приведён список важнейших атрибутов полиморфного класса, которые наследуются всеми его потомками. К ним относятся: массив указателей на аргументы pInput[j], массив возвращаемых функцией результатов Output[k] и массив параметров функции Param[n]. Размерность массивов задается значениями параметров конструкторов потомков, которые, в свою очередь, передаются им через интерфейс createBlock COM-сервера (см. табл. 2).
| Таблица 1 |
| Атрибуты полиморфного класса - общего предка всех математических классов |
| CBlkTemplate.pInput[j] |
| CBlkTemplate.Output[k] |
| CBlkTemplate.Param[n] |
| CBlkTemplate.Calc() = 0; // virtual |
| CBlkTemplate. ... |
делает возможным (в графическом представлении) их соединение линиями связи в требуемом порядке. Эта операция осуществляется через интерфейс createWire COM-сервера (см. табл. 2). Её результатом является присвоение значения указателя на элемент массива Output[k] одного объекта элементу массива pInput[j] другого объекта (см. цепочку повторяющихся фрагментов на рис. 3). Таким образом, совокупность показанных программных решений делает возможным создание моделей систем из любого требуемого набора математических функций, между которыми возможна любая требуемая схема передачи аргументов.
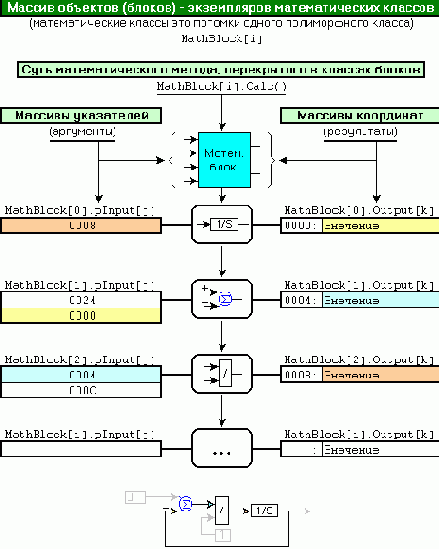
Рис. 3
В целях ознакомления с интерфейсами математического ядра (COM-сервера) рассмотрим программу на VB, которая создает модель динамической системы и запускает процесс симуляции в пакетном режиме (для расшифровки параметров методов см. табл. 2).
Листинг 2
' Объявляем переменную, как математическое ядро
Private WithEvents Mdl As SimKernel Private mySmplArr(100) As Double
' Создаём из COM-сервера объект - математическое ядро
Set Mdl = CreateObject("Klinachyov.SimKernel")
' Устанавливаем свойства симуляции модели
Mdl.setSimProp 0, 1, 0.01, 0
' Создаем блоки (математические объекты или функции)
Mdl.createBlock L702, 0, 1, 0 ' inpVector
Mdl.createBlock L101, 2, 1, 2 ' summingJunction
Mdl.createBlock L100, 1, 1, 1 ' gain
Mdl.createBlock L951, 1, 1, 1 ' 1/S
Mdl.createBlock L802, 1, 0, 0 ' outVector
Mdl.createBlock L800, 2, 0, 0 ' export
' Устанавливаем параметры блоков и начальные условия
Mdl.setBlkParam 2, 1, 1 Mdl.setBlkParam 2, 2, -1 Mdl.setBlkParam 3, 1, 4 Mdl.setBlkParam 4, 1, 0
' Создаем связи между блоками (схему передачи аргументов)
Mdl.createWire 1, 1, 1, 2 Mdl.createWire 2, 1, 1, 3 Mdl.createWire 3, 1, 1, 4 Mdl.createWire 4, 1, 2, 2 Mdl.createWire 2, 1, 1, 6 Mdl.createWire 4, 1, 2, 6 Mdl.createWire 4, 1, 1, 5
' Устанавливаем очередность исполнения блоков
Mdl.BildSimFlow
' Это не важно - задаем массив выборок для обработки моделью
For i = 0 To 99 mySmplArr(i) = Sin(i / 7) Next
' Передаем массив в математическое ядро
Mdl.swapInputOutputSamples mySmplArr
' Запускаем процесс симуляции модели
Mdl.Simulation
' Считываем обработанный моделью массив
Mdl.swapInputOutputSamples mySmplArr
' Запускаем сервер визуализации результатов
' ...
Беглого взгляда на программу достаточно, дабы сделать вывод о том, что процесс создания модели унифицирован (для создания любого математического блока или же любой межблочной связи используется только один соответствующий метод (интерфейс)). Именно жесткая унификация интерфейсов делает возможным создание шлюзов между редакторами векторной графики и математическими ядрами.
 Интерфейсы (методы) COM-сервера - математического ядра Интерфейсы (методы) COM-сервера - математического ядра |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |