Алгоритмы программ цифровых фильтров
Существует три основных алгоритма программной реализации дискретных передаточных функций (z-ПФ):
| Алгоритм | Требуемое быстродействие | Объём памяти |
 а) с двумя буферами б) с одним буфером |
24(m+k+1) / Tц | 9m+9k+12 |
 |
52k / Tц | 20k+10 |
 |
50k / Tц | 19k+8 |
Дискретную ПФ можно представить в любой из форм:
 |
W(z
) = |
 |
Y(z) |   |
b0+b1z-1+...+bmz-m | - стандартная форма для дискретных ПФ |
 |
 |
|||||
| X(z) | a0+a1z-1+...+akz-k |
 |
W(z
) = |
 |
Y(z) |   |
K |  |
1+e2z-1 |   |
1+ekz-1 | - разложение z-ПФ на множители [1] |
 |
 |
 |
 |
|||||||
| X(z) | 1+d1z-1 | 1+d2z-1 | 1+dkz-1 |
 |
W(z
) = |
 |
Y(z) |   |
P1 |   |
P2 |   |
Pk | - разложение z-ПФ на элементарные дроби [1] |
 |
 |
 |
 |
|||||||
| X(z) | 1+d1z-1 | 1+d2z-1 | 1+dkz-1 |
где: ei - нули z-ПФ; di - полюса z-ПФ; a0 - не равно нулю; Pi
- коэффициенты разложения
Этим формам представления z-ПФ соответствуют структурные схемы изображенные на рис. 1.
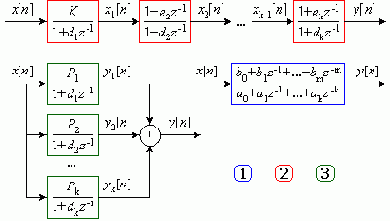
Рис. 1
Разложения
делают параметры z-ПФ независимыми, позволяют контролировать ряд дополнительных фазовых координат: x1[n], x2[n], ..., xk-1[n]; или y1[n], y2[n], ..., yk[n]
- что удобно при отладке систем.
Последовательная структура
удобна при синтезе дискретной коррекции.
Параллельная структура
удобна для построения цифровых регуляторов.
Разложение z-ПФ на элементарные дроби
позволяет реализовать z-ПФ на параллельно работающих ЦВМ для повышения быстродействия.
Перечисленные факторы определяют выбор алгоритма программы для ЦВМ.
После разложений, каждый из множителей в форме
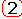
или каждую из элементарных дробей в форме
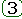
следует представить в стандартной форме
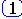
(с отрицательными степенями оператора z). Переход к разностным уравнениям будет един. z-ПФ в форме
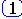
соответствует разностное уравнение (РУ):
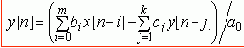
по которому и составляется программа. Поскольку текущее значение выходной координаты y[n] рассчитывается по предыдущим значениям y[n-1], y[n-2], y[n-k]
- данное РУ называется рекурсивным.
Изобразим структурную схему цифрового фильтра для этого уравнения (см.
рис. 2). Ее можно преобразовать, объединив два буфера (см. рис. 3). Цепочки элементов z-1 в программах будут соответствовать буферам из ячеек памяти, данные в которых сдвигаются на каждом такте дискретизации. Обе структурные схемы можно составить из простейших блоков программы VisSim.
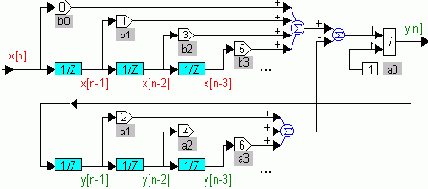
Структурной схеме соответствует алгоритм
Условие физической реализуемости - а0 № 0
Рис. 2
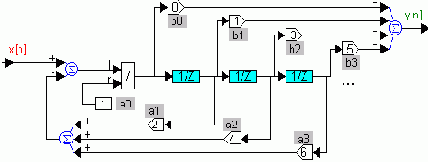
Структурной схеме соответствует алгоритм
Условие физической реализуемости - а0 № 0
Рис. 3
Если выбран последовательный
или параллельный
алгоритм, то структура каждого множителя или элементарной дроби первого порядка (см. рис. 1) будет иметь более простой вид (см. рис. 4).
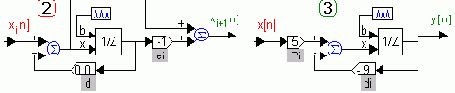
Рис. 4
Согласно структурной схеме рис. 2, составим процедуру реализующую дискретную ПФ второго порядка:
function y_zW(x) { y=( k * (x*b0+xz_1*b1+xz_2*b2) - ( yz_1*a1+yz_2*a2) ) / a0; xz_2=xz_1; xz_1=x; yz_2=yz_1; yz_1=y; return y; };
где: xz_2, xz_1 и yz_2, yz_1 - ячейки двух буферов, т.е. регистры задержки - z -1.
Выберем коэффициенты z-ПФ для расчета переходной характеристики и построим ее:
| K= | |||||
| b0= | b1= | b2= | |||
| a0= | a1= | a2= |