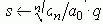
Пусть имеем характеристическое уравнение:

a0 s n + a1

s n-1 + ... + an-1 s + an

= 0 .

Приведем его к нормированному виду (разделим на an

и выполним подстановку

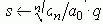
q n + a1/an

(W0 q) n-1 + ... + ak/an (W0

q) n-k +...+ 1 = 0 ,

где: 

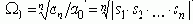
- среднегеометрический корень.

вызовет пропорциональное радиальное смещение корней. Т.е. вид переходного процесса меняться не будет, но будет меняться его временной масштаб. Поэтому среднегеометрический корень W0 является мерой быстродействия.

Для приведенного уравнения время будет безразмерным

t = W0 t, переходная функция h(t) в случае кратных вещественных корней или одной пары комплексных будет ограничена минорантой и мажорантой:

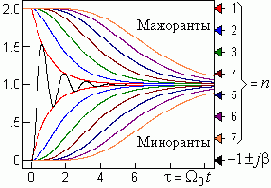
где: u(h, t) = e -ht [1 + (ht)1/1! + (ht)2/2! + ... + (ht)n-1/(n-1)! ]

- разложение в ряд Тейлора огибающей той составляющей в пререходном процессе, корень которой ближе к оси "+j".

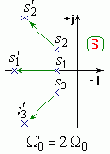
На рис. демонстрируется, что любой переходный процесс в любой системе будет затухать тем медленней, чем больше корней вблизи оси "+j".