Гидравлические исполнительные устройства
3.6. ГИДРАВЛИЧЕСКИЕ ИСПОЛНИТЕЛЬНЫЕ УСТРОЙСТВА
Гидравлические исполнительные устройства (ГИУ) в сравнении с электрическими (ЭИУ) обладают следующими преимуществами:
самосмазываемость ГИУ, работающих на минеральных маслах, что повышает износостойкость и надежность работы;
способность развивать большие крутящие моменты и усилия с помощью малогабаритных и легких устройств; удельные силы ГИУ больше удельных сил ЭИУ в 10 ... 20 раз;
малая инерционность движущихся рабочих органов ГИУ, что обеспечивает высокое быстродействие и высокую точность работы следящего привода с ГИУ. При рабочем давлении 30 МПа и мощности более 1 кВт отношение крутящего момента к моменту инерции ротора ГИУ в 20 ... 30 раз больше, чем соответствующее отношение ЭИУ;
автоматическое предохранение ГИУ от перегрузки, реализуемое с помощью простых и надежных устройств (предохранительных клапанов);
простота реализации возвратно-поступательного движения без промежуточных устройств (гидроцилиндров);
высокая жесткость к нагрузке за счет существенно большей жесткости гидравлической «пружины», определяемой геометрией ГИУ и модулем упругости рабочей жидкости, по сравнению с жесткостью электромагнитной «пружины» в ЭИУ. Как недостатки ГИУ отметим следующие:
жесткие требования к точности изготовления элементов ГИУ, так как от рабочих зазоров в узлах ГИУ зависят утечки и перетечки и, следовательно, КПД ГИУ;
сложность проблемы обеспечения чистоты рабочей жидкости.
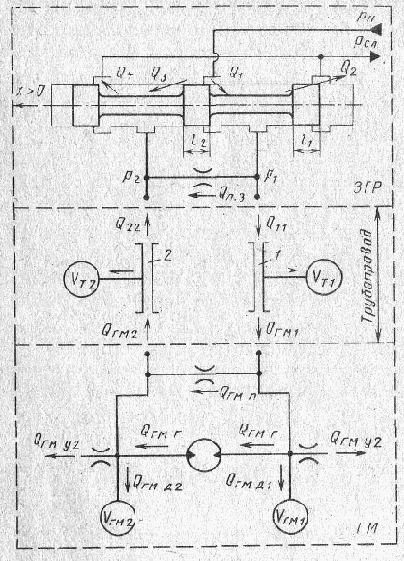
Рис. 37. Принципиальная схема ГПД
В качестве ГИУ в гидравлических следящих приводах (ГСП) применяются гидроприводы (ГП) с дроссельным и объемным регулированием скорости выходного звена.
Гидропривод с дроссельным регулированием (ГПД). В ГПД скорость выходного звена регулируется изменением площади приходного сечения дросселя. ГП этого класса отличаются простотой конструкции, малыми массами и размерами, высоким быстродействием, надежностью работы, малой стоимостью. В силу этого ГПД получил наибольшее распространение в системах управления летательными аппаратами, в транспортной технике, в станкостроении, судостроении и в целом ряде других областей техники.
Как недостатки ГПД следует отметить малый КПД, зависимость скорости выходного звена от нагрузки, зависимость основных характеристик от температуры рабочей жидкости.
ГПД состоит из исполнительного механизма (гидроцилиндр, полноповоротный или неполноповоротный гидромотор) и управляющего гидравлического дросселирующего устройства, в качестве которого наибольшее распространение в различных областях техники получил четырехщелевой (четырехдроссельный) золотниковый гидрораспределитель (ЗГР) (рис. 37). В высококачественных ГСП на основе ГПД применяются ЗГР, близкие к «идеальным» (с малыми перекрытиями A по рабочим кромкам; ? = (2 ... 5)?, где ? = (2 ... 9) мкм — радиальный зазор между золотником и гильзой). Такие ЗГР обеспечивают высокую чувствительность ГПД к управляющему сигналу и малые утечки рабочей жидкости.
Главной особенностью работы ГПД является то, что перепад давлений ?p0 — ?p, где ?p0 = рн — рсл — располагаемый (начальный) перепад давлений; ?p = р1—р2 — перепад давлений в рабочих полостях ГИУ; рн — давление нагнетания; рсл — давление слива, полностью срабатывается на гидравлических сопротивлениях ЗГР, и если, например, ГПД работает на холостом ходу (?p = 0), то вся мощность гидравлического потока превращается в теплоту. Этим объясняется низкий КПД ГПД и, как следствие, использование их в ГСП, мощность которых в большинстве случаев не превышает 5 кВт. Тем не менее, известны многочисленные примеры использования ГПД для ГСП существенно большей мощности, когда главным считается минимизация массы и размеров, надежность и быстродействие, а КПД не имеет существенного значения (летательные аппараты).
Рассмотрим расчетную схему ГПД с исполнительным механизмом в виде гидромотора (ГМ) (см. рис. 37).
Примем следующие допущения:
1) температура рабочей жидкости (РЖ) постоянная;
2) перекрытия в ЗГР равны нулю;
3) коэффициент расхода рабочих окон ЗГР постоянный;
4) гидравлические проводимости рабочих окон ЗГР при одинаковых смещениях золотника относительно нейтрального положения равны;
5) гидравлическими сопротивлениями и волновыми процессами в трубопроводе пренебрегаем ( длина трубопровода не более 15 м);
6) модуль упругости РЖ постоянный (не зависит от давления); в принципе модуль упругости РЖ зависит от давления, но при p > 0,8 ... 1 МПа и при содержании газовой фазы в РЖ менее 0,1 % его можно считать постоянным [4];
7) расходами, обусловленными компрессией и декомпрессией РЖ при прохождении рабочей камеры через разделительную перемычку распределительного узла, ГМ, пренебрегаем;
8) массой РЖ, находящейся в трубопроводе, пренебрегаем;
9) работу предохранительных клапанов не учитываем (считаем, что нагрузка на валу ГМ не превышает максимальную расчетную нагрузку);
10) вал ГМ считаем абсолютно жестким;
11) конструкция ГМ симметричная. Условимся также, что расчетная схема, изображенная на рис. 37, соответствует x > 0, где x — координата ЗГР.
Расходы Q2 и Q3 (при x > 0) будем учитывать с помощью расхода перетечек QП.3 через условный дроссель (см. рис. 37). B соответствии с расчетной схемой
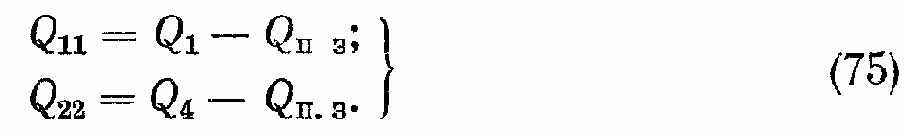
Здесь QП.3 = kQp (р1 — р2) — расход перетечек, характеризующий объемные потери ЗГР;

где bщ — ширина щели ЗГР; ? — радиальный зазор ЗГР; ?Д — коэффициент динамической вязкости РЖ;
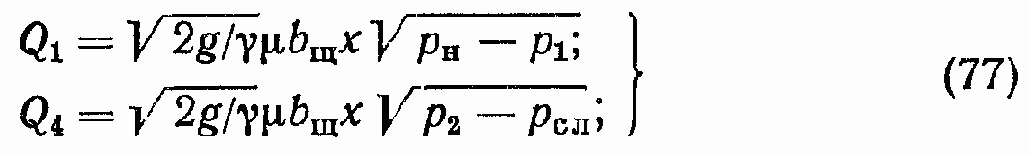
? — коэффициент расхода рабочих окон ЗГР; этот коэффициент зависит от числа Рейнольдса (Re) [4], но при Re > 260 можно считать ? = const = 0,71; g — ускорение свободного падения; ? — плотность РЖ.
Введем обозначение
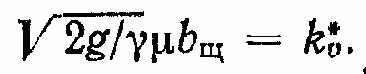
Перейдем к рассмотрению уравнений ГМ. Расчетная схема ГМ как часть общей расчетной схемы ГПД приведена на рис. 37. Входными величинами для ГМ являются расходы РЖ QГМ.1 и QГМ.2. поступающей в ГМ и выходящей из него, выходной величиной — угловая скорость ? вала ГМ, а возмущением — момент нагрузки на валу ГМ.
Запишем уравнение расходов ГМ:

Здесь QГМ.г — геометрическая подача ГМ;

где WГМ = VГМ р/(2?) — характерный объем ГМ; VГМ р — рабочий объем ГМ (изменение объема рабочих камер ГМ за один оборот вала); QГМ yl и QГМ y2 — расходы утечек из приемной и отдающей полостей ГМ:
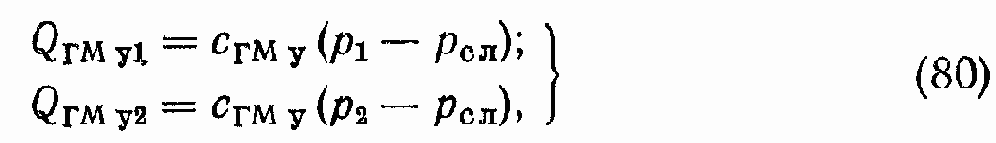
где сГМу — коэффициент утечек ГМ; для аксиально- поршневых гидромашин сГМу может быть определен по формуле
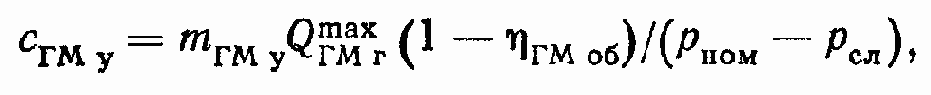
где mГМу = 0,6 ... 1,2 — коэффициент, зависящий от конструкции ГМ;
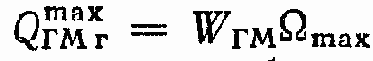
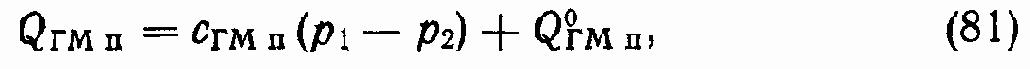
где сГМп — коэффициент перетечек ГМ;
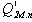
для аксиально-поршневых ГМ
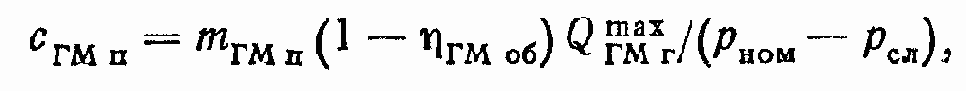
где mГМ.п = 0 ... 0,4 — коэффициент, зависящий от конструктивного исполнения распределительного узла ГМ; QГМ д1 и QГМ д2 — расходы, обусловленные сжимаемостью РЖ, находящейся в отдающей (сливной) и в приемной полостях ГМ;

где VГМ1 и VГМ2 - объемы РЖ, находящейся в приемной и в отдающей полостях ГМ; в силу обычной симметричности конструкции ГМ VГМ1 = VГМ2 = VГМ.
Систему уравнений (78) с учетом уравнений (79)—(83) можно записать:

Уравнение моментов на валу ГМ
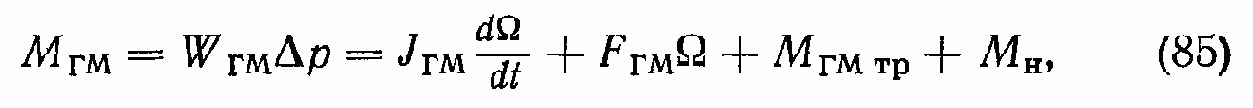
где МГМ — момент, развиваемый ГМ; JГМ — момент инерции ротора ГМ; FГМ — коэффициент вязкого трения в ГМ; МГМ тр — момент трения в ГМ; MН — момент нагрузки на валу ГМ;
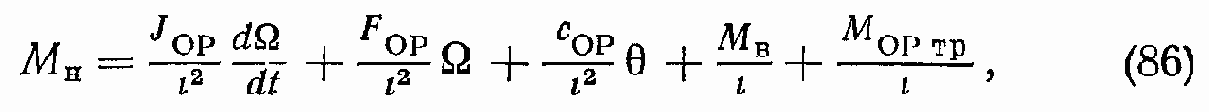
где JОР — момент инерции объекта регулирования; (OP)i — передаточное число редуктора между ГМ и OP; FОР — коэффициент вязкого трения OP; сОР — жесткость пружинной (шарнирной нагрузки) OP; ? — угол поворота вала ГМ; МВ — внешний возмущающий момент, действующий на OP; MОP тр — момент трения на OP.
Рассмотрим уравнения трубопровода. При принятых допущениях трубопровод можно рассматривать как систему с сосредоточенными параметрами. Для трубопровода (при x > 0) справедливы следующие уравнения:

Здесь Vт1 и Vт2 — объемы РЖ, находящейся в трубопроводах 1 и 2,

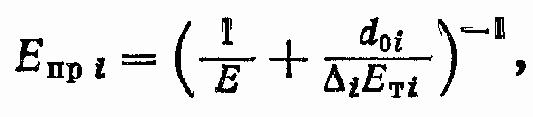
где d0i — внутренний диаметр i-го трубопровода; ?i — толщина стенок i-го трубопровода; ETi — модуль упругости материала стенок i-го трубопровода.
Решая совместно уравнения (75), (77), (84) и (87) для x > 0, получаем
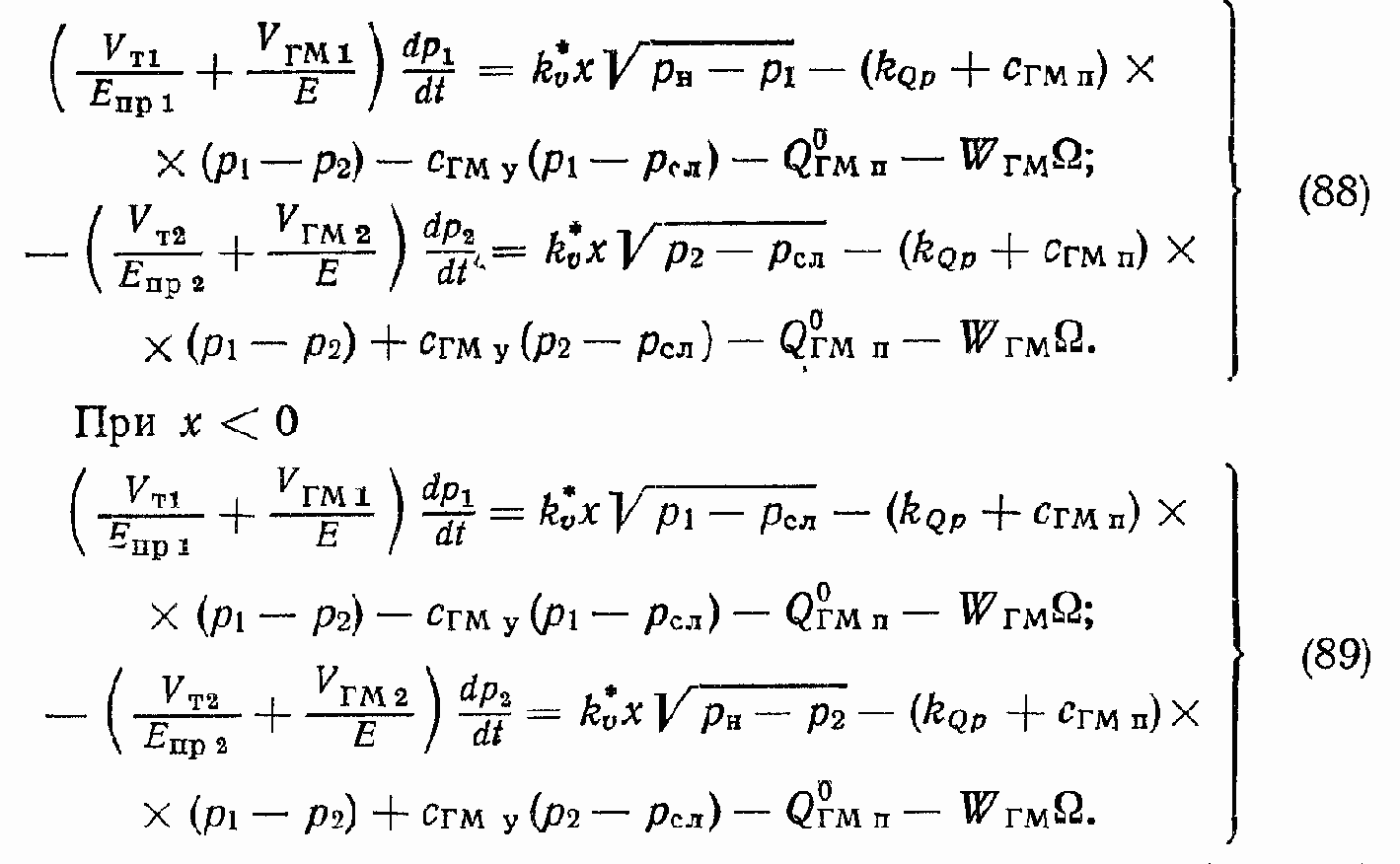
Уравнения (88) и (89) совместно с уравнениями (85) и (86) дают связь между координатами x и ? для ГПД с исполнительным механизмом в виде ГМ при учете параметров ГП и параметров нагрузки. Если в качестве исполнительного механизма рассмотреть гидроцилиндр (ГЦ), то в уравнениях (88) и (89) необходимо ввести следующие изменения.
Геометрическая подача
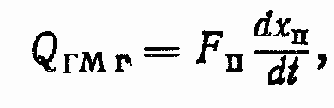
где FП— площадь поршня ГЦ; dxП/dt — скорость выходного звена (штока) ГЦ.
Соответственно расходы
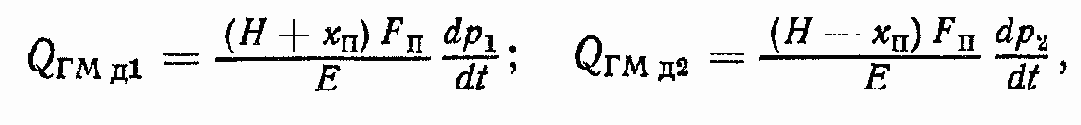
где Н — максимальное перемещение поршня от среднего положения,
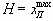
Для ГЦ сГМу = 0, Q0ГМ.п = 0; обозначим
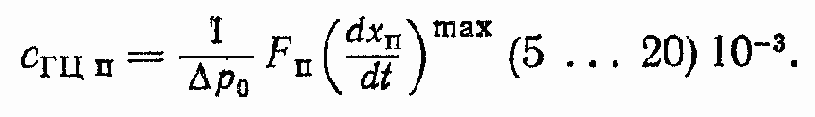
Уравнение сил для ГЦ записывается в следующем виде:

где M — масса OP и подвижных частей ГЦ; kД - коэффициент вязкого демпфирования OP; kП — коэффициент пружинной (шарнирной) нагрузки OP; РОР тр — сила трения в OP; Ргц тр — сила трения в ГЦ; РВ — внешнее возмущение, действующее на OP (не зависит ни от хП, ни от dx/dt, ни от d2xП/dt2).
C учетом указанных различий уравнения (88) и (89) примут вид
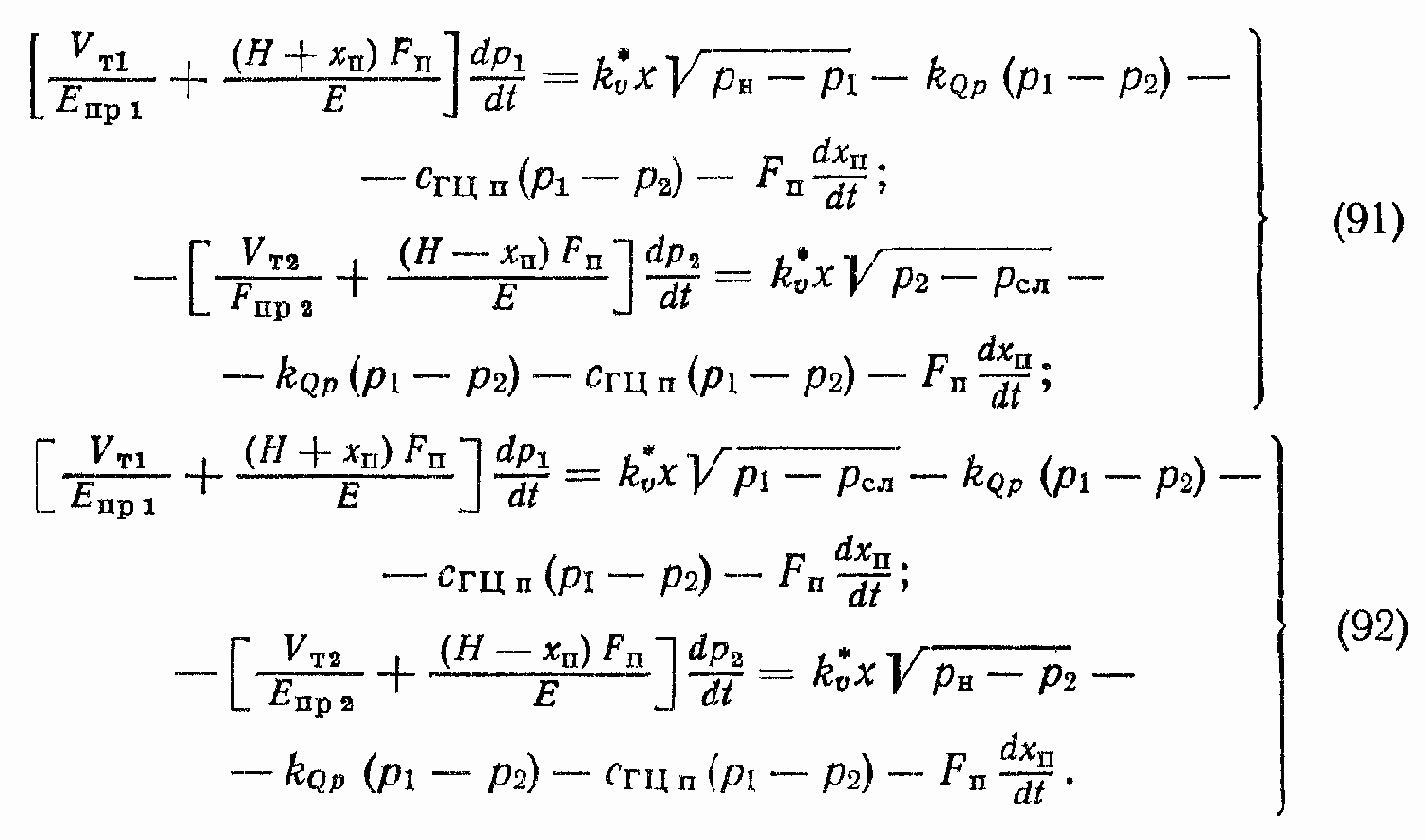
Примечание. Если в ГПД ограничение по скорости обеспечивается площадью окон ЗГР, то при работе ГПД в режимах, когда | x | > хmax, где хmax— значение координаты x, при котором наступает ограничение по dxП/dt, в уравнениях (91), (92) вместо координаты x будет фигурировать хmax.
Системы уравнений (88), (89) и (91), (92) — сложные нелинейные системы, которые могут быть решены только с помощью ЭВМ.
Примечания: 1. Ограничимся в дальнейшем рассмотрением ГПД с ГЦ как наиболее часто встречающуюся в практике схему ГПД. 2. Bo многих работах по ГПД рассматривается жесткость сг гидравлической «пружины», под которой подразумевается отношение внешней силы, приложенной к штоку ГЦ, к значению «просадки» координаты хП под действием этой силы при условии, что рабочие полости ГЦ полностью герметизированы (нет перетечек через золотник и поршень и нет утечек). Приращение объема первой полости ГЦ при давлении p1 будет

Соответствующее перемещение поршня

Тогда выражение для жесткости первой полости ГЦ представим так:
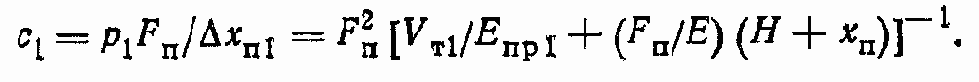
Аналогично для второй полости ГЦ
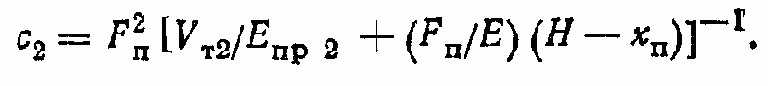
Суммарная жесткость c?г = с1 + с2, т. e.
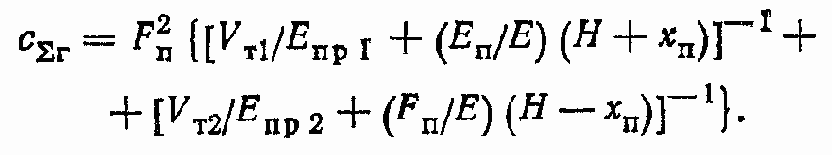
Минимальное значение c?г реализуется при хП = 0:

Если VT1 = VT2 = VT; VT= qHFП; q = const; ЕПР1= ЕПР1= ЕПР2= rЕ, где r < 1, то
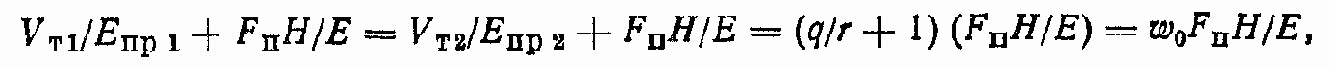
где W0 = (q/r+ 1).
Минимальная жесткость
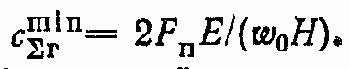
Рассмотрим частный случай: хП = 0 (поршень в среднем положении). Как правило, гидролинии делаются одинаковой длины из труб одного диаметра при одинаковой толщине стенок, поэтому можно считать, что VT1/EПР1 = VT2/EПР2.
Введем обозначение:
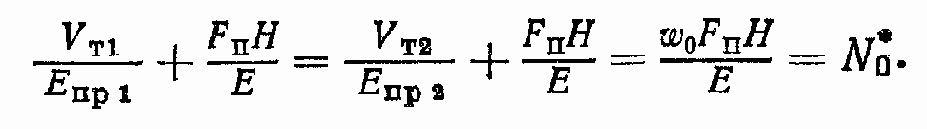
Рассмотрим уравнения (91) с учетом принятых допущений:
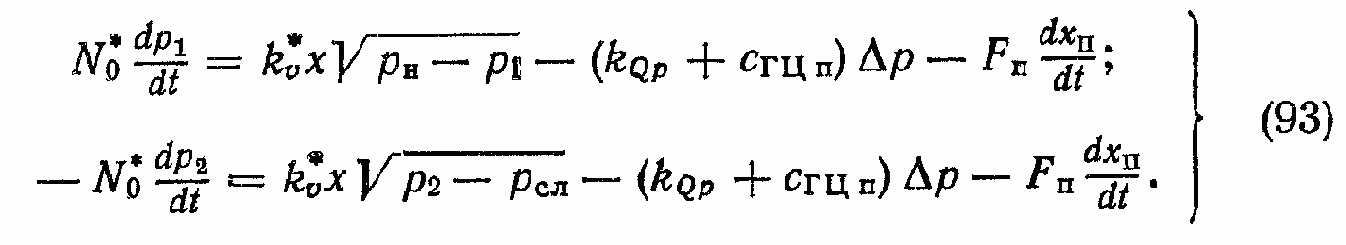
Вычтем из первого уравнения второе:
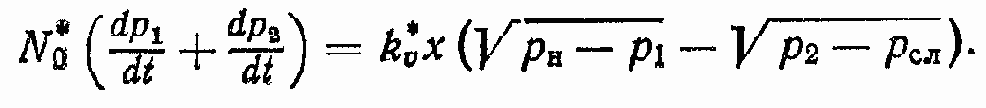
Рассмотрим dp1/dt + dp2/dt. Производные dp1/dt и dp2/dt характеризуют скорость изменения давлений p1 и р2. И хотя сами величины p1 и p2 могут отличаться друг от друга, в силу принципа работы ГЦ и принятых допущений (VT1/EПР1 = VT2/EПР2; хП= 0) можно заключить, что знаки этих производных противоположны, а модули равны. Следовательно, dp1/dt + dp2/dt = 0. Тогда

или

Аналогичное равенство можно получить и из системы (92) при тех же допущениях.
Решая совместно систему уравнений:

получим
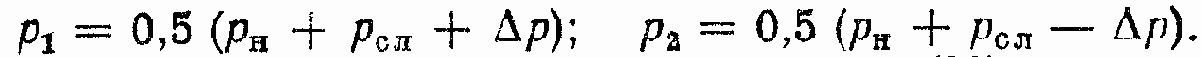
Подставляя эти значения р1 и р2 в уравнения (93), а затем складывая эти уравнения и деля результат на два, получим
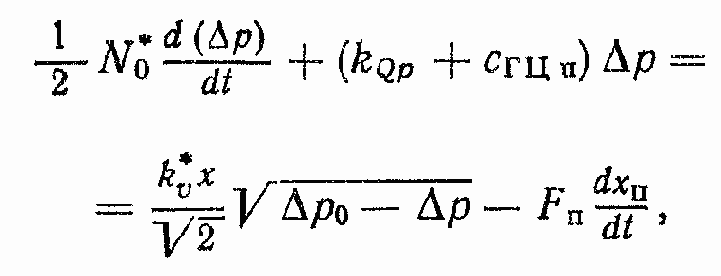
где ?p0 = рн — рсл.
Аналогичные операции с системой уравнений (92) дают

Последние два уравнения можно записать в виде одного уравнения
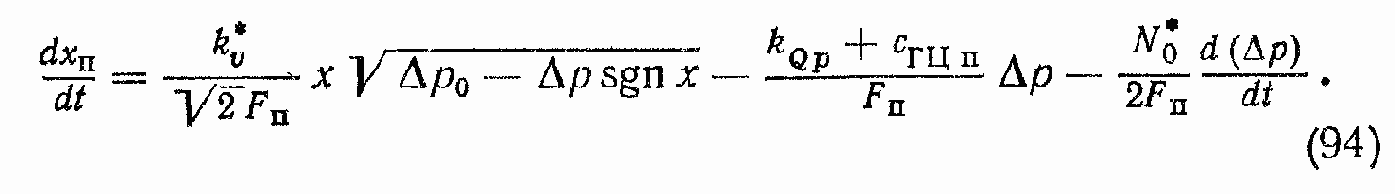
Примечания: 1. Как и при рассмотрении систем уравнений (91) и (92), зона работы ЗГР |x|> xmax может быть учтена простой подстановкой в уравнение (94) хmax вместо x. 2. Для случая, когда в ГПД используется ГМ в предположении, что сГМ.у = 0, уравнение (94) имеет тот же вид, только вместо FП фигурирует WГМ, а вместо dxП/dt — скорость ?
Решая уравнение (94) совместно с уравнением (90), получаем одно уравнение, устанавливающее связь координаты x с выходной координатой ГПД хП при учете параметров нагрузки M, kД, kП, PВ, РГЦтр, МОРтр и параметров привода


Уравнение (95) заменяет систему уравнений (90), (91) и (92), и хотя оно существенно проще решается на ЭВМ, для качественного анализа влияния параметров привода и нагрузки на устойчивость замкнутого контура ГСП с ГПД и для инженерного расчета динамических характеристик необходимо перейти к линейным дифференциальным уравнениям. Прежде чем перейти к рассмотрению линейной модели ГПД, сделаем следующие замечания:
1. Изменяющиеся в функции координаты хП объемы VГЦ1 (хП) и VГЦ2 (хП) рабочей жидкости в рабочих полостях ГЦ при анализе устойчивости замкнутого контура ГСП с ГПД и при расчете динамических характеристик можно не учитывать, так как при хП = 0 (VГЦ1 = VГЦ2 = FПH) динамические характеристики ГПД наихудшие, а запас устойчивости замкнутого контура ГСП с ГПД наименьший. Поэтому расчет динамических характеристик ГПД и расчет устойчивости ГСП с ГПД, проводимые при хП = 0, дают определенные запасы по сравнению с точной моделью (при хП = var).
2. При расчете статических характеристик зависимость VГЦ1 и VГЦ2 от хП можно также не учитывать, так как эта зависимость проявляется только в динамических процессах (dp1/dt ? 0; dp2/dt ? 0). Поэтому при изучении статических характеристик уравнение (95) можно использовать без всяких допущений.
Перейдем к рассмотрению линейной модели ГПД. Главной нелинейностью уравнения (95) является радикал
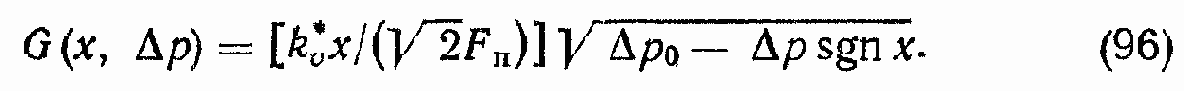
Специальные исследования, проведенные на цифровой ЭВМ, показали, что радикал (96) может быть заменен следующим линейным выражением:
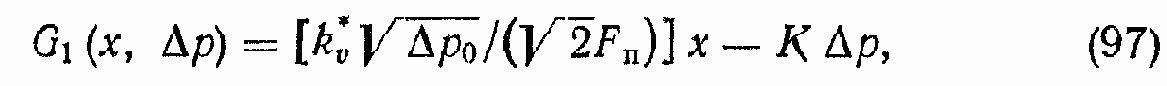
в котором коэффициент K. выбирают по следующему правилу:
1) K = 0 при расчете устойчивости замкнутого контура ГСП с ГПД;
2)
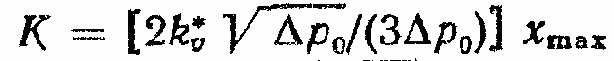
При этом устойчивость и динамические характеристики рассчитывают с определенными, допустимыми в инженерных расчетах, запасами.
Запишем уравнение (94) с учетом замены радикала G (х, ?р) на G1 (х, ?р):
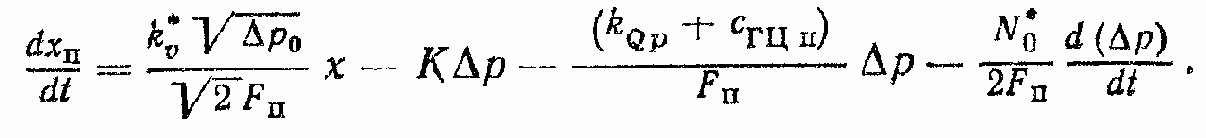
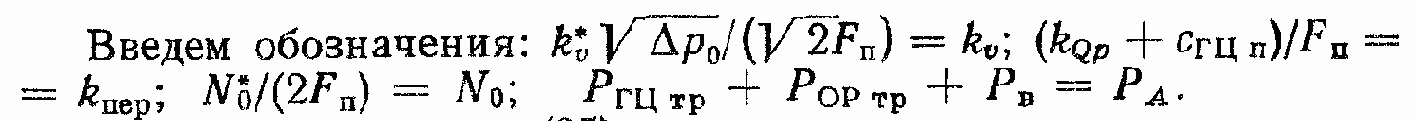
Запишем уравнение (95) с учетом линеаризации радикала и введенных обозначений:
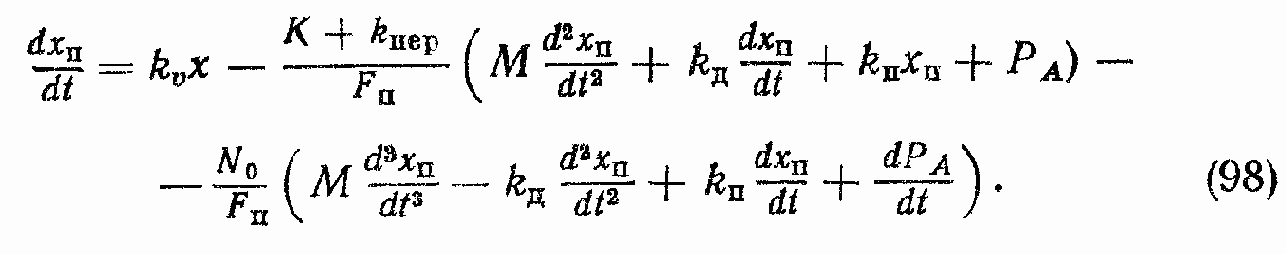
Последнее уравнение в операторной форме записывается в следующем виде:
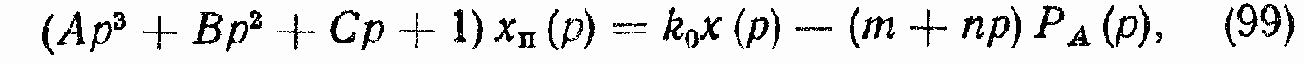
где
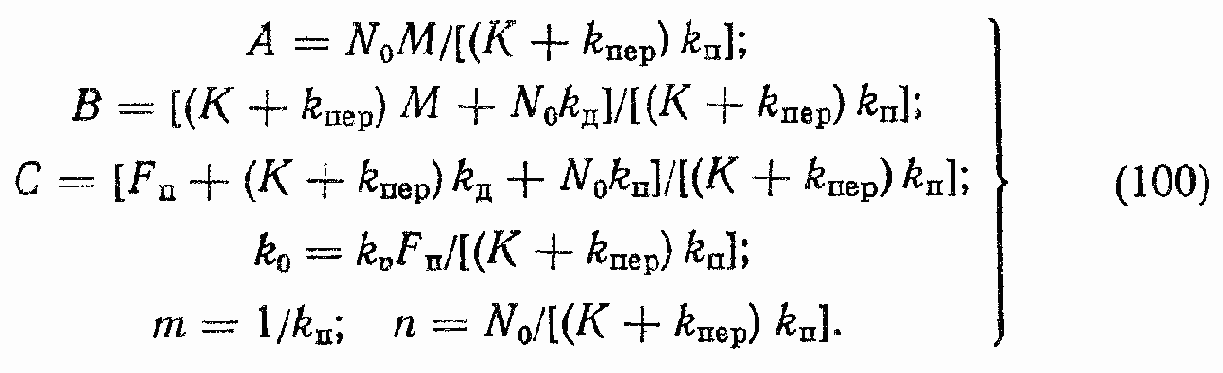
Соответствующая уравнению (99) структурная схема ГПД приведена на рис. 38, а. Эту схему удобно представить так, как показано на рис. 38, б, т. e. с использованием простейших звеньев. Ha этой схеме основные параметры определяются по следующим формулам:


Рис. 38. Структурные схемы ГПД
Большой практический интерес представляет случай, когда в уравнении (98) kП = 0. При этом уравнение (99) принимает вид
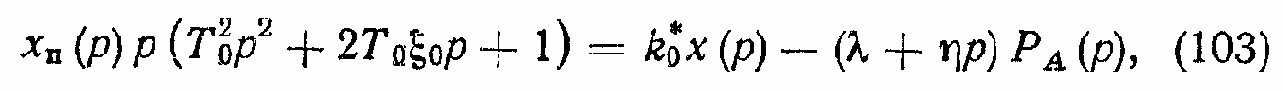
где
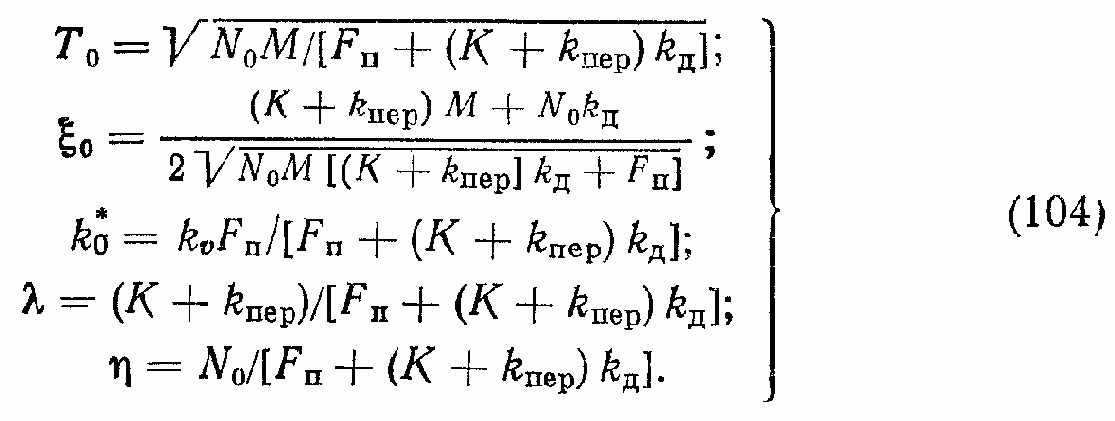
Соответствующая структурная схема изображена на рис. 38, в.
Введем обозначение:
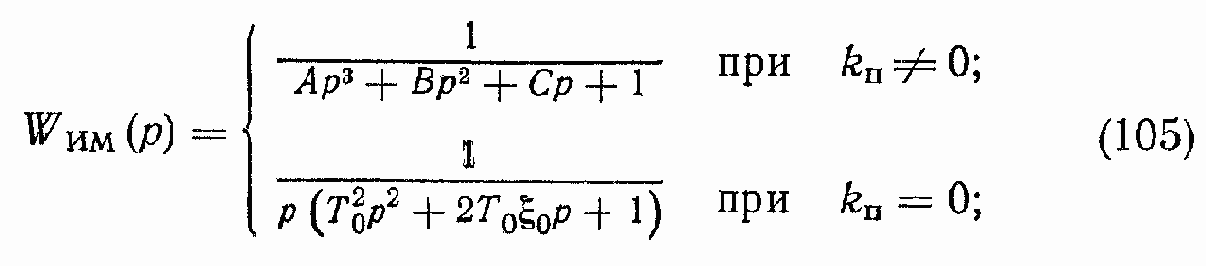
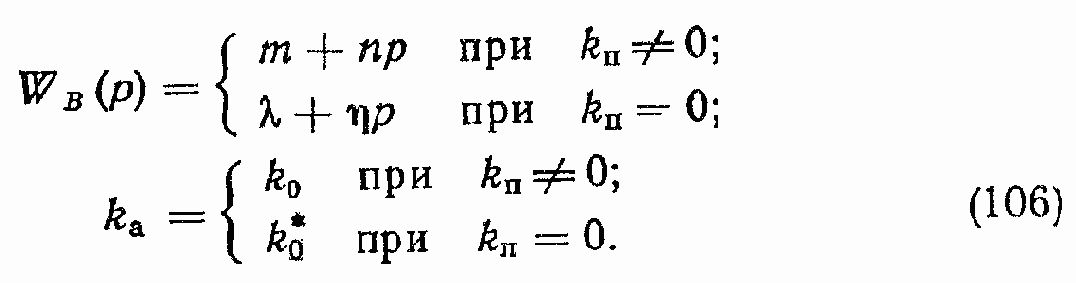
Тогда основные передаточные функции ГПД могут быть записаны в следующем виде:
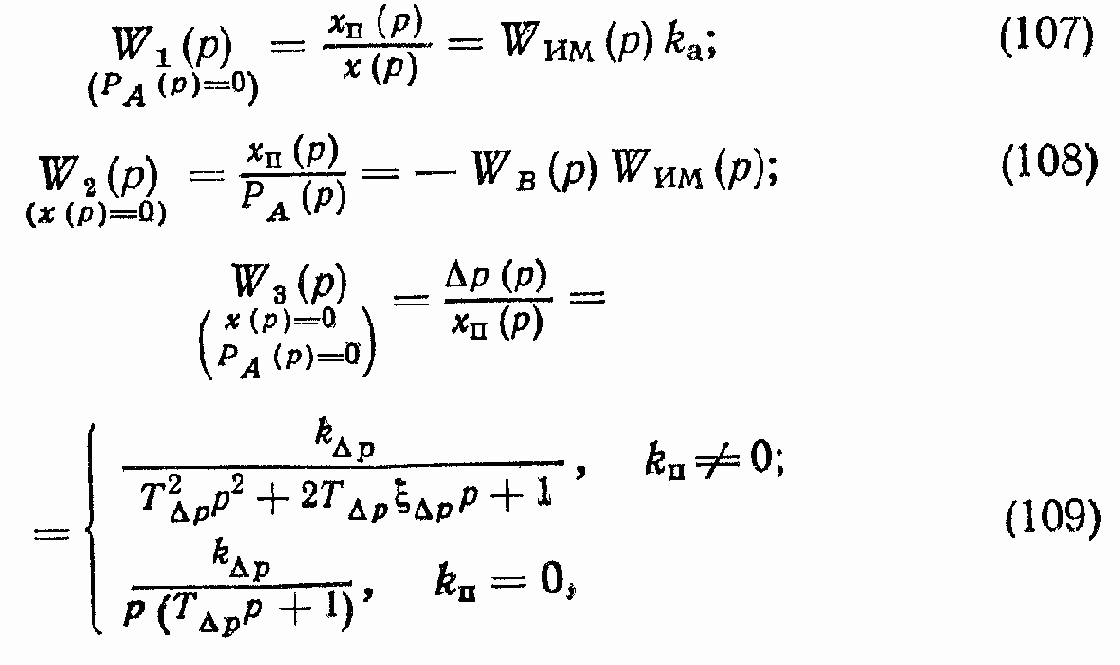
где

Статические характеристики ГПД (механическую, регулировочную скоростную и регулировочную характеристику по перепаду давлений) легко получить из уравнения (94). Следует отметить, что уравнения статических характеристик для ГПД с ГМ и ГПД с ГЦ будут различаться только обозначениями: там, где для ГЦ фигурирует площадь поршня FП и скорость штока dxП/dt, для ГМ в уравнения необходимо подставить WГM и ?. Поэтому при рассмотрении статических характеристик ограничимся случаем, когда в ГПД используется ГЦ.
Механическая (нагрузочная) характеристика

определяет функциональную зависимость скорости выходного звена (штока ГЦ) в установившемся режиме от координаты x ЗГР и от перепада давлений ?р.
Уравнения механической характеристики:
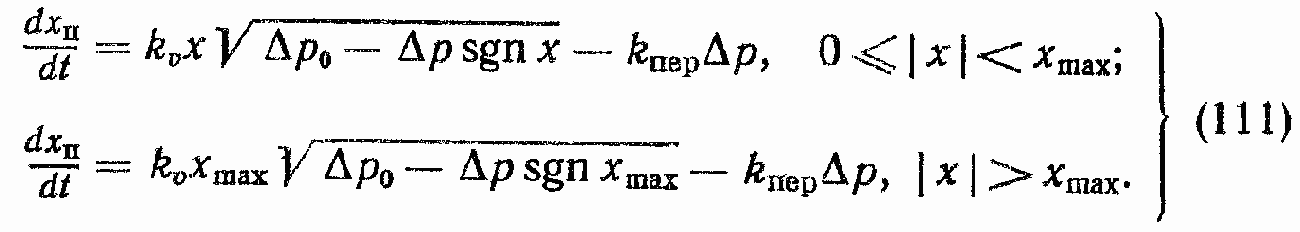
График механической характеристики приведен на рис. 39, а.
Регулировочная скоростная характеристика (скоростная характеристика холостого хода) определяет функциональную зависимость скорости выходного звена ГЦ в установившемся режиме от координаты x при отсутствии нагрузки (?р = 0). Уравнение этой характеристики получается из уравнения (111) при ?р = 0:
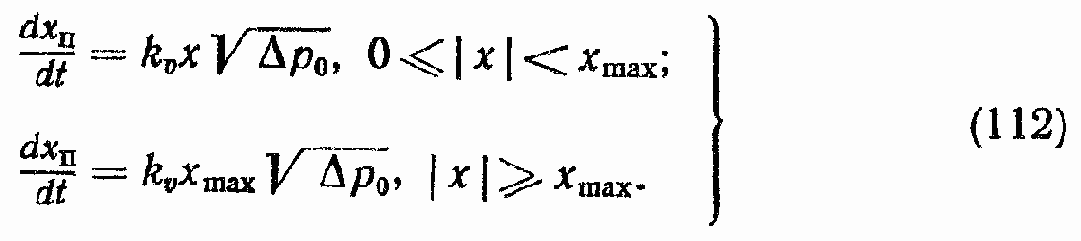
График регулировочной характеристики по скорости приведен на рис. 39, б.
Регулировочная характеристика по перепаду давлений (силовая характеристика) определяет функциональную зависимость перепада давлений ?р при неподвижном (заторможенном) выходном звене ГЦ (dxП/dt = 0) от координаты x. Уравнение регулировочной характеристики по перепаду давлений можно получить из уравнения (111) при dxП/dt = 0:
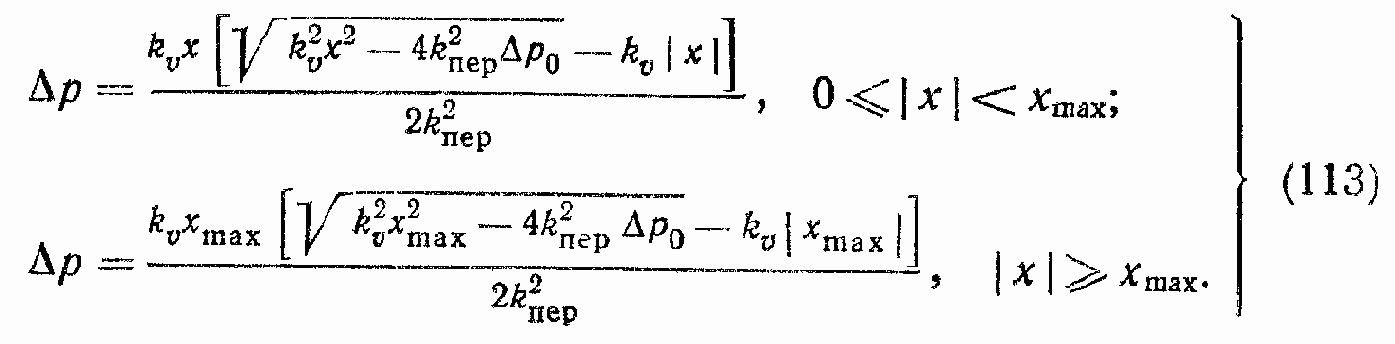
График регулировочной характеристики по перепаду давлений, построенный для конкретных значений kv, kпер, хmax, изображен на рис. 39, в.
Полезная мощность ГПД может быть определена по механической характеристике

или
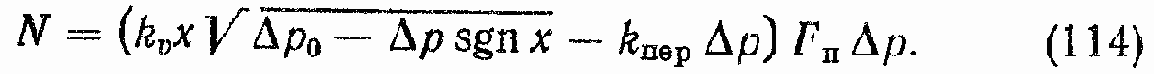
Последнее выражение кроме мощности определяет также зависимость КПД ГПД от ?р в некотором масштабе, так как
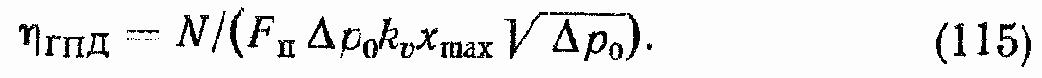
Как полезную мощность, так и КПД ГПД рассчитывают при х =хmax
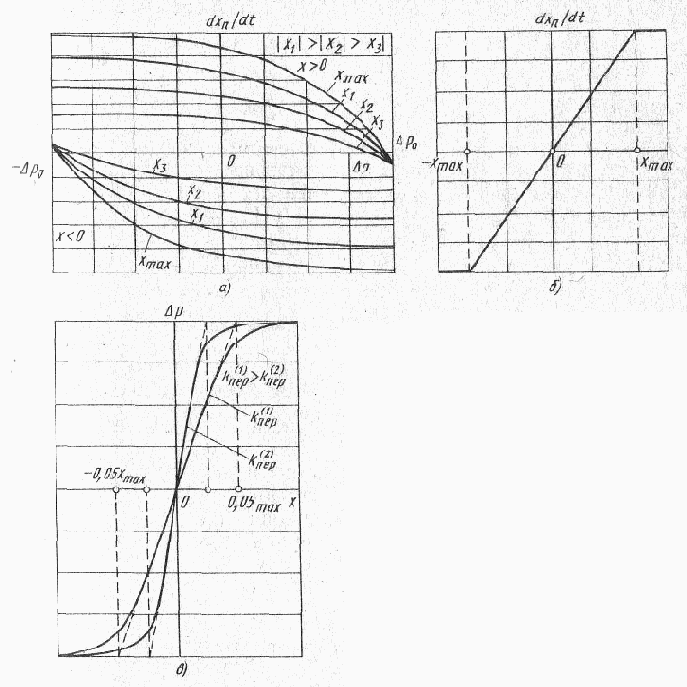
Рис. 39. Статические характеристики ГПД
При kпер = 0 максимальное значение мощности и КПД ГПД реализуется при ?р = 2/3?р0.
Ha практике (при учете kпер) максимальный КПД ГПД обычно не превышает 0,3.
Гидропривод с объемным регулированием (ГПО). По сравнению с ГПД ГПО обладает более высоким КПД и более жесткой механической характеристикой Как недостатки ГПО по сравнению с ГПД отметим более сложную конструкцию и меньшее быстродействие. Основными элементами ГПО являются насос и гидродвигатель (ГД). В ГПО наибольшее распространение получили аксиально-поршневые насосы с наклонным блоком цилиндров и с наклонным диском (шайбой), хотя известны случаи использования в ГПО пластинчатых насосов однократного действия и радиально-поршневых насосов, регулирование подачи которых обеспечивается за счет изменения эксцентриситета. В качестве ГД в основном применяются ГМ (аксиально-поршневого типа и радиально-поршневого; реже шестеренные и пластинчатые) и ГЦ. Иногда в качестве ГД используются неполноповоротные ГМ и квадранты.
Примечание. Учитывая, что ГЦ подробно описан в разделе ГПД, ограничимся в дальнейшем рассмотрением ГПО с исполнительным механизмом в виде ГМ.
В ГПО скорость выходного звена можно регулировать либо путем изменения рабочего объема насоса при постоянном рабочем объеме ГМ, либо путем изменения рабочего объема ГМ при постоянном рабочем объеме насоса, либо одновременным изменением рабочих объемов насоса и ГМ (рис. 40).
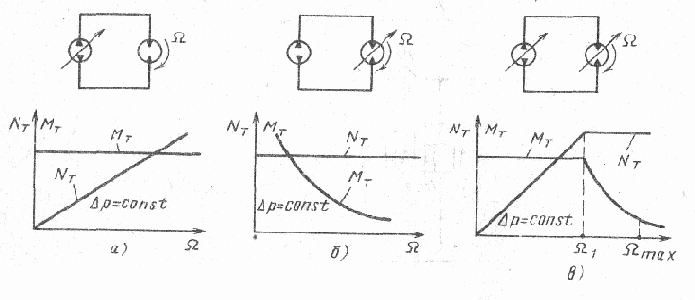
Рис. 40. Принципиальные схемы ГПО
Наибольшее распространение в технике получил первый способ (рис. 40, а), при котором теоретическое значение момента Мт на валу ГМ при постоянной нагрузке (?р = const, где ?р — перепад давлений между гидролиниями ГПО) остается постоянным при росте угловой скорости ГМ.
Теоретическое значение мощности N4, на валу ГМ при ?р = const изменяется линейно в функции от ?. Второй способ регулирования скорости (рис. 40, б) применяют в системах, где необходимо изменять момент на валу ГМ в широком диапазоне при ограниченной мощности ГПО. Третий способ (рис. 40, в) реализуется в так называемых двухканальных следящих системах, в которых один канал (регулирование ГМ) обеспечивает грубое регулирование в диапазоне скоростей от максимального значения ? max до ? 1, а другой канал (регулирование насоса) позволяет точно регулировать скорость в диапазоне от ? 1 до ? = 0. Более точное регулирование во втором случае обеспечивается за счет работы следящей системы при постоянном (максимальном) моменте Мт. B дальнейшем ограничимся рассмотрением первого способа регулирования ГПО.
ГПО с регулируемым насосом H работает следующим образом (рис. 41), При поступлении на вход механизма управления МУ управляющего сигнала Uупр происходит отклонение регулирующего органа PO насоса от нейтрального положения на угол, значение которого пропорционально модулю сигнала Uупр, a знак (направление отклонения PO) — знаку этого сигнала. При отклонении PO от нейтрального положения насос подает определенный расход РЖ, пропорциональный углу ? отклонения PO, в определенный трубопровод, например в гидролинию 1, которая в этом случае называется напорной гидролинией. Одновременно всасывающая полость насоса соединяется с гидролинией 2 (гидролиния низкого давления). РЖ от насоса через гидролинию 1 поступает в приемную полость ГМ. Отдающая полость ГМ через гидролинию 2 соединена с приемной полостью насоса. При таком соединении насоса и ГМ обеспечивается определенная угловая скорость вала ГМ, пропорциональная модулю |Uупр| управляющего сигнала и соответствующая (по направлению вращения вала ГМ) знаку Uупр.
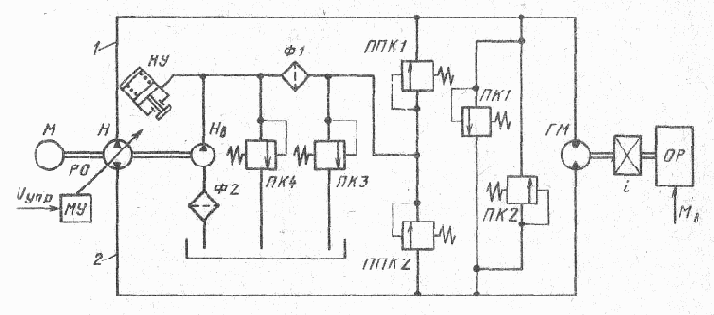
Рис. 41. Принципиальная схема ГПО первого типа
В процессе работы замкнутого гидравлического контура (насос— гидролинии — ГМ) неизбежны объемные потери РЖ, для восполнения которых предназначен вспомогательный насос Нв, приводимый в движение, как и основной насос, от приводного двигателя M.
Подпитка гидролиний осуществляется через подпиточные клапаны ???1 и ???2. Переливной клапан ПК3 поддерживает в системе подпитки определенное давление рП = (2 ... 2,5) МПа, при котором подпиточные клапаны ???1 и ???2 обеспечивают давление всасывания в гидролиниях 1 и 2 рВС = (0,7 ... 1,3)МПа.
Для предохранения системы подпитки при засорении фильтра ?1 она снабжается предохранительным клапаном ??4. Иногда кроме фильтра ?1 на линии нагнетания устанавливается фильтр ?2 на линии всасывания вспомогательного насоса. Для защиты приводного двигателя от перегрузки ГПО снабжается нуль установителем НУ, который устанавливает PO в нулевое положение при падении давления подпитки в результате аварийной ситуации (например, нарушения герметичности гидролиний ГПО). Для предохранения ГПО от перегрузок предусмотрены предохранительные клапаны ??1 и ??2, отрегулированные на максимально допустимый перепад давлений ?рmax. Гидромотор через редуктор с передаточным числом i приводит во вращение объект регулирования OP, на который действует внешний возмущающий момент Мв.
Рассмотрим основные уравнения насоса как элемента ГПО. Входной величиной для насоса является параметр регулирования e.
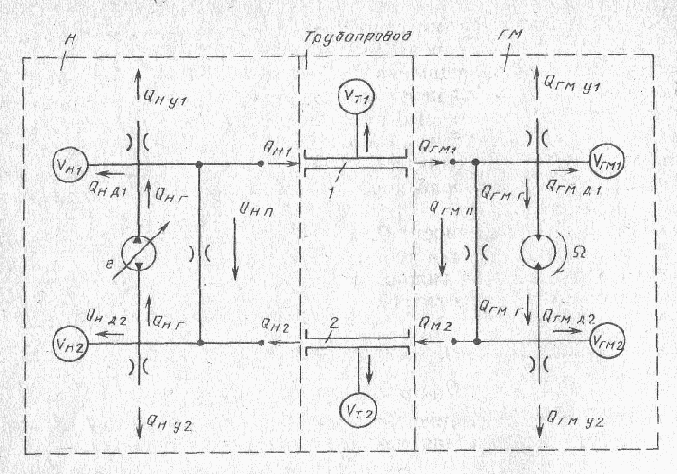
Рис. 42. Расчетная схема ГПО
Параметр регулирования аксиально-поршневого насоса с наклонным блоком цилиндров определяют по формуле
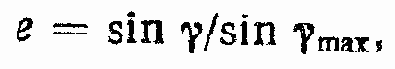
где ? — угол наклона блока цилиндров.
Если насос аксиально-поршневого типа с наклонным диском, то
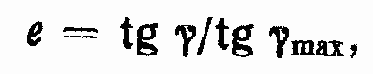
где ? — угол наклона диска.
И, наконец, параметр регулирования радиально-поршневого насоса и регулируемого пластинчатого насоса однократного действия рассчитывают по формуле
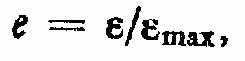
где ? — эксцентриситет насоса. В дальнейшем ограничимся рассмотрением аксиально-поршневых машин.
Выходными величинами насоса будем считать расходы QH1 и QH2 рабочей жидкости, выходящей из насоса и поступающей в него соответственно. Перепад давлений р1—р2 в гидролиниях 1 и 2, вызванный нагрузкой на ГМ, будем рассматривать как внешнее возмущение. Расчетная схема насоса как часть расчетной схемы ГПО показана на рис. 42.
Примем следующие допущения: 1) расходами, обусловленными процессами компрессии и декомпрессии РЖ при прохождении рабочей камеры H через разделительные перемычки распределительного узла, пренебрегаем; 2) температура РЖ постоянная; 3) гидравлическими сопротивлениями и волновыми процессами в гидролиниях пренебрегаем; 4) модуль E РЖ считаем постоянным (не зависящим ни от давления, ни от температуры); 5) работу системы подпитки не учитываем (рсл = 0); 6) мощность приводного двигателя неограниченная; 7) конструкции насоса и ГМ симметричные; 8) вал ГМ абсолютно жесткий; 9) массой РЖ, находящейся в гидролиниях, пренебрегаем; 10) условимся, что расчетная схема, изображенная на рис. 42, соответствует случаю, когда e > 0.
При учете сжимаемости РЖ, находящейся в рабочих камерах насоса, а также утечек и перетечек уравнения для QH1— расхода РЖ, поступающей в гидролинию 1, и QH2 — расхода РЖ, поступающей в насос из гидролинии 2, могут быть записаны в следующем виде:
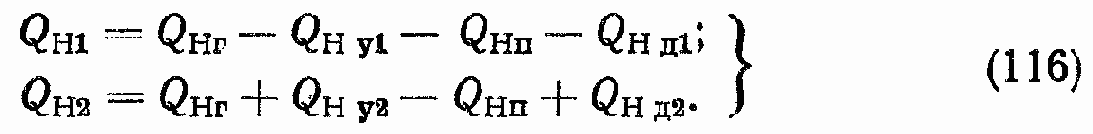
Рассмотрим составляющие этой системы уравнений:
QHг — геометрическая подача насоса;

где ?? — характерный объем насоса;

VНp — рабочий объем насоса — изменение объема рабочих камер насоса за один оборот его вала при e = 1 (при максимальном отклонении PO); ?? — угловая скорость вала насоса;
QНу1 — расход утечек из отдающей полости насоса; QНу2 — расход утечек из приемной полости насоса;
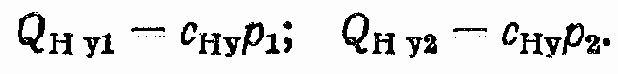
Здесь сНу — коэффициент утечек насоса; для аксиально-поршневых насосов коэффициент утечек может быть определен по формуле
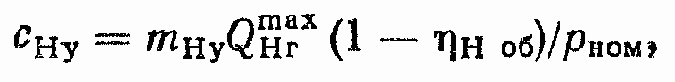
где mНу = 0,6... 1,2 — коэффициент, зависящий от конструкции насоса;
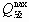
QHп — расход перетечек (из гидролинии 1 в гидролинию 2) через распределитель;
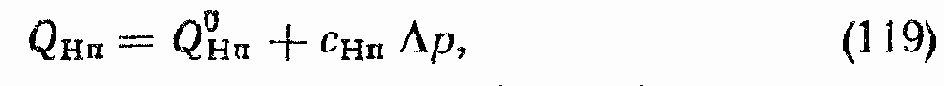
где
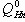
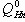

где mНп = 0 … 0, 5 зависит от конкретного конструктивного исполнения распределительного узла насоса;
QН.д1, QН.д2— расходы РЖ, обусловленные сжимаемостью РЖ, находящейся в приемной и в отдающей камерах насоса;
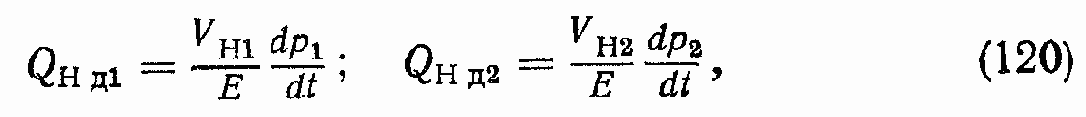
где VH1, VH2 — объемы РЖ, находящейся в приемной и в отдающей камерах насоса; в силу обычной симметричности конструкции насоса VH1 = VH2 = VH; E — модуль упругости РЖ.
Запишем систему уравнений (116) с учетом уравнений (117)— (120):
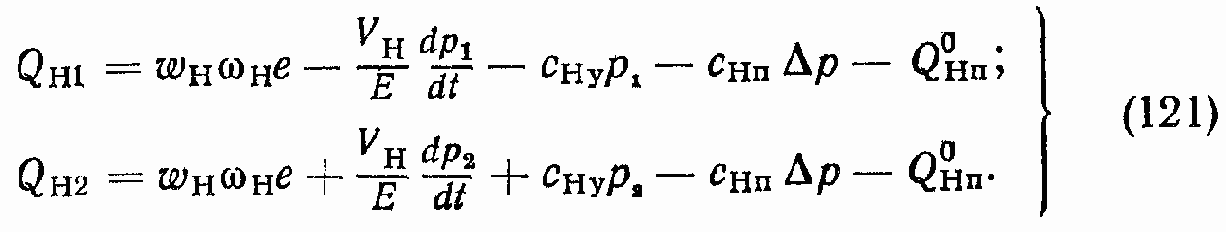
Уравнения ГМ и гидролиний были рассмотрены в параграфе, посвященном ГПД (см. уравнения (78)—(87), в которых вместо QН1 фигурирует Q11и вместо QH2 — Q22)·
Уравнения (116)—(121) совместно с уравнениями расходов ГМ и гидролиний позволяют записать уравнения расходов для ГПО (система насос – гидролинии – ГМ):
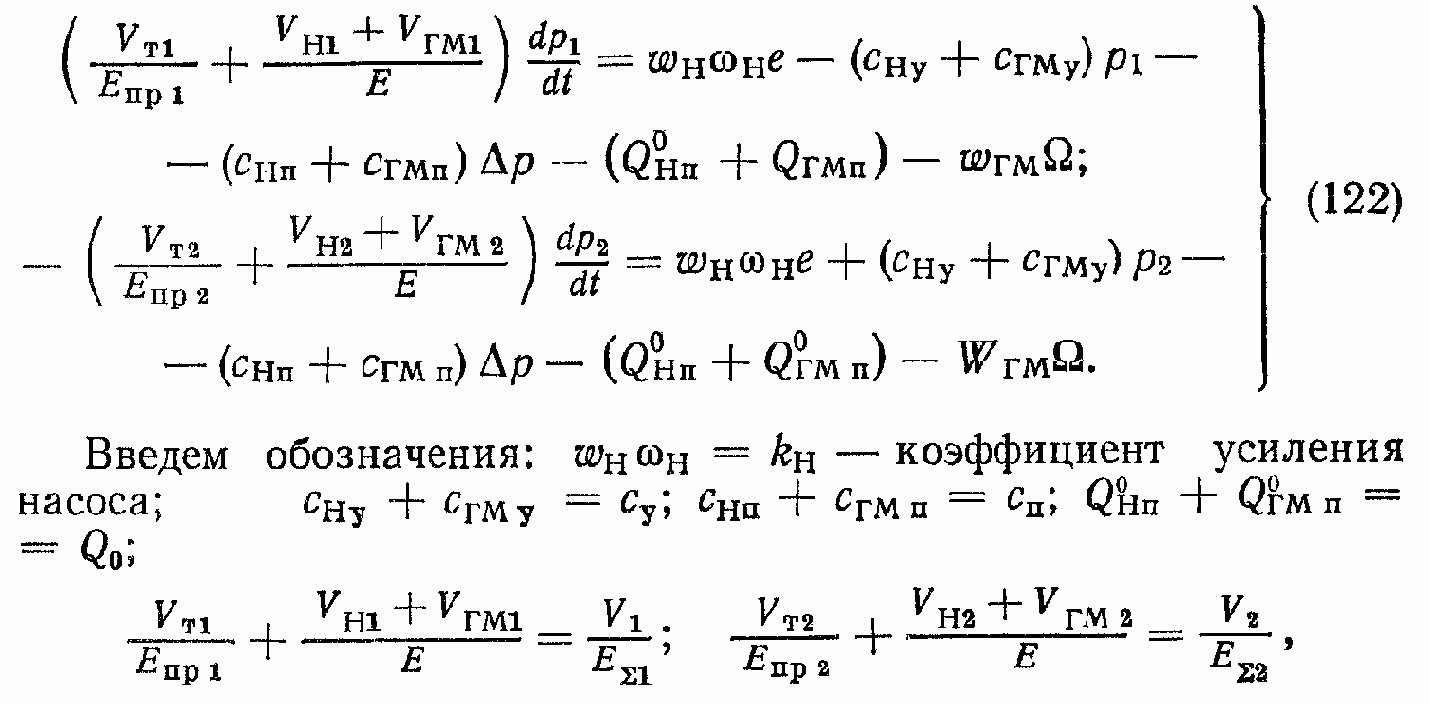
где
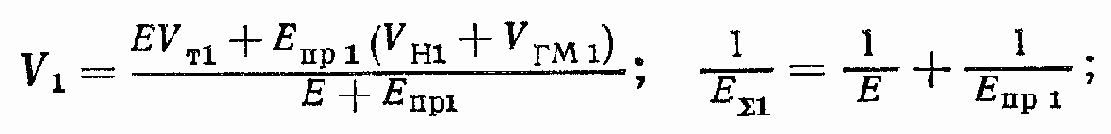
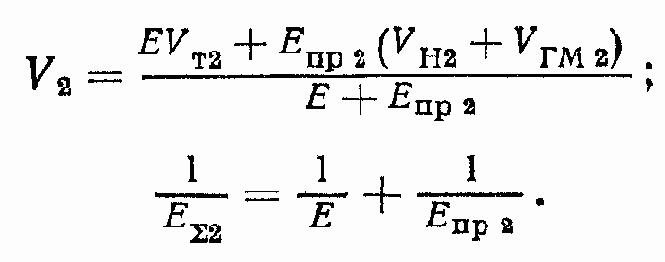
Уравнение (122) совместно с уравнениями (85) и (86) позволяет установить зависимость ? от параметра регулирования e с учетом параметров нагрузки и параметров ГПО.
Перейдем к рассмотрению упрощенной математической модели ГПО. Примем допущение, что гидролинии выполнены из одинаковых трубопроводов (ЕПР1 = ЕПР2; VT1 = VT1 = VT). Следовательно, ??1 = ??2 = ??. B силу обычной симметричности конструкций насоса и ГМ V1 = V2 = V.
C учетом последнего допущения и принятых выше обозначений система (122) примет вид

Сложим уравнения системы (123) и результат разделим на два:
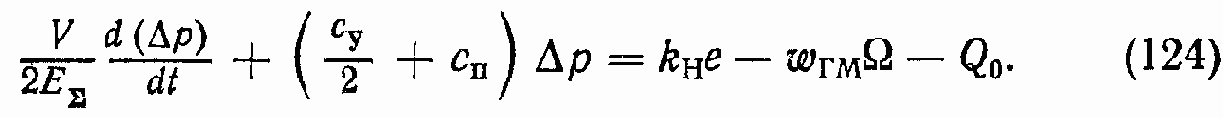
Введем обозначения (в соответствии с [1]):

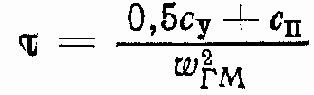
Тогда уравнение (124) примет вид

Или в операторной форме

Если воспользоваться очевидным уравнением Мгм = шгм ?p, то уравнение (126) можно представить в следующем виде:
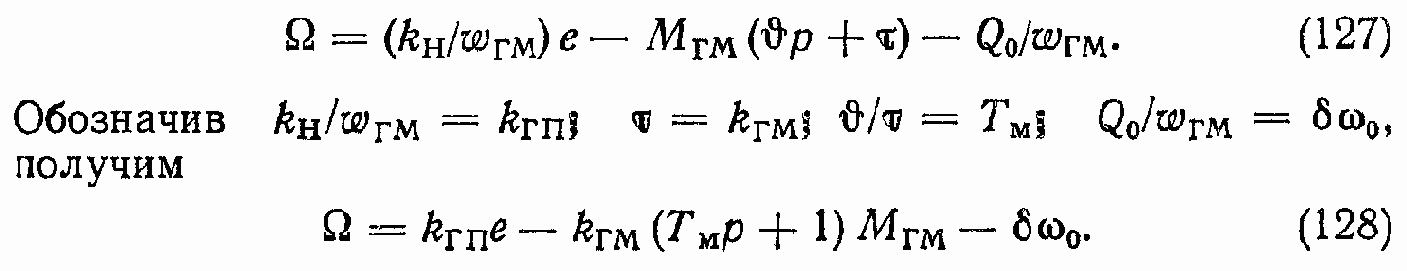
При e < 0
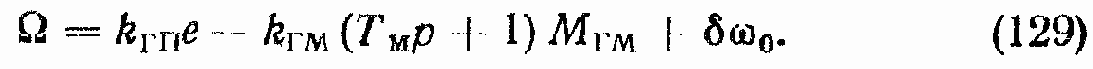
Объединяя уравнения (128) и (129), получим
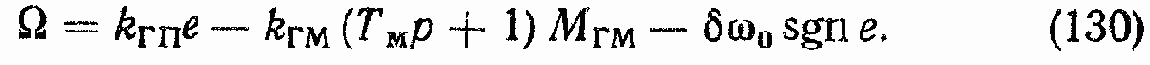
Последнее уравнение устанавливает связь между угловой скоростью ? вала ГМ, параметром регулирования e, моментом МГМ нагрузки на валу ГМ и параметрами kГП, kГМ, ТМ и ??0 ???.
Решая совместно уравнения (130), (85) и (86) при сОР = 0, получим

Или с учетом ? = ?p
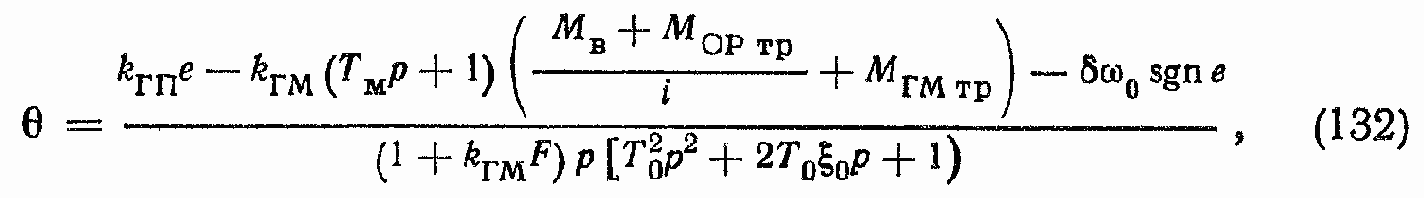
где
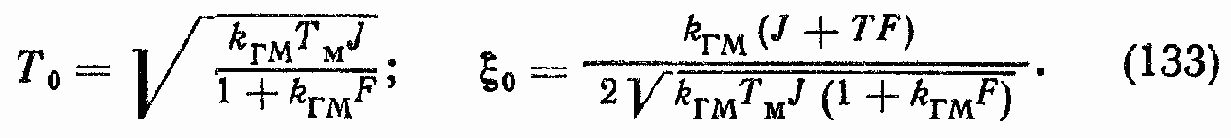
Или с учетом, что kГМ = ? и ТМ = ?/?, получим
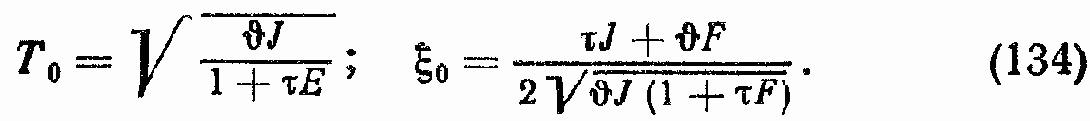
B формулах (133) и (134) J = JГМ + JОР/i2; F = FГМ + FОР/i2. Если сОР ? 0, то связь между координатой ? и параметром регулирования может быть описана с помощью следующей формулы:
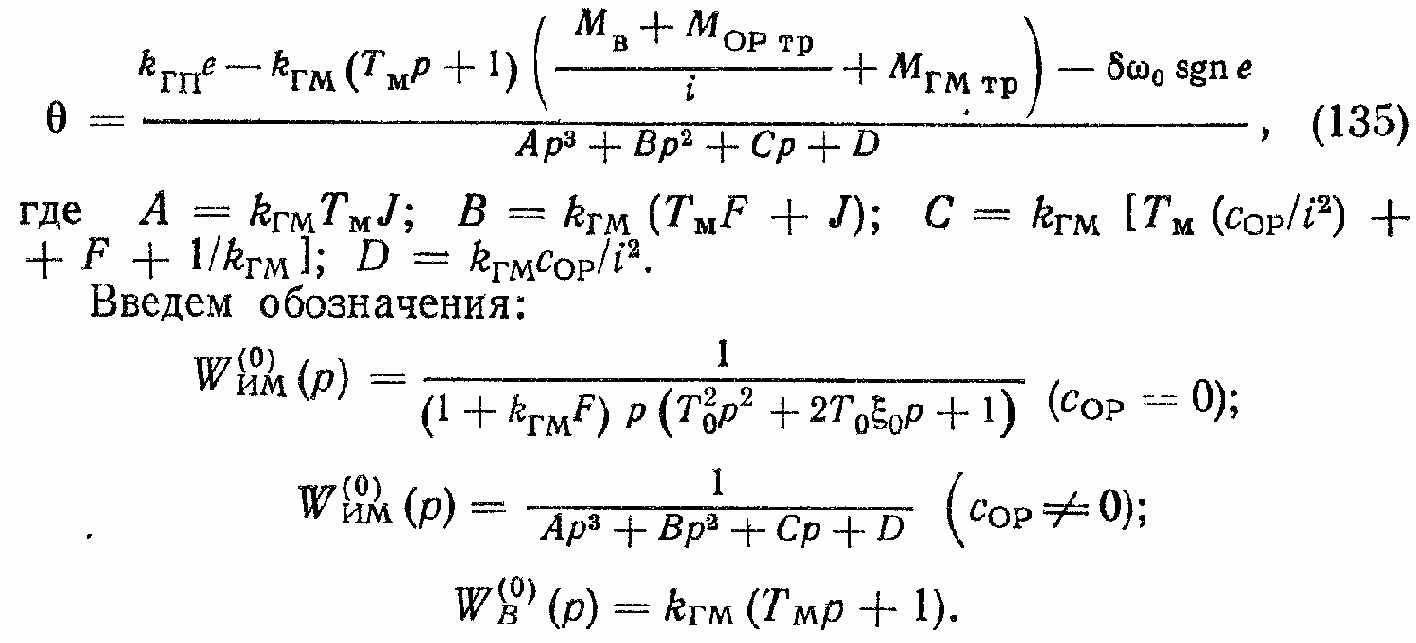
В соответствии с уравнениями (132) и (135) структурные схемы ГПО могут быть представлены так, как показано на рис. 43.


Рис. 43. Структурные схемы ГПО: а – при сОР = 0; б – при сОР ? 0
Примечание. При анализе динамических характеристик ГПО при e > 0,05 в уравнениях (131), (132) и (135) принимают ??0 = 0. Эту величину учитывают только при изучении статических характеристик ГПО и при расчете динамики специальных режимов работы (на «ползучих» скоростях).
Запишем основные передаточные функции ГПО при MОP.тр = MГМ.тр = 0.

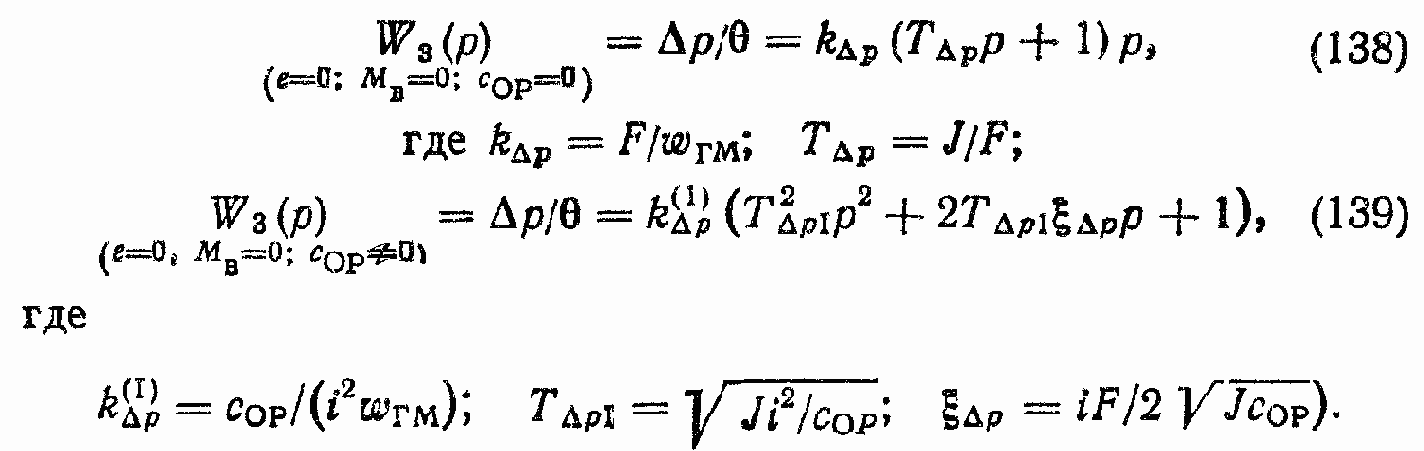
Пример 3. Рассчитать передаточные функции ГПО W1(p) и W2(p).
Основные данные ГПО (см. табл. ?5 прил.): ГПО с регулируемым насосом, параметры которого ?Н = 22,6 см3/рад; ?Н = 150 рад/с; VН1 = VН2 = VН = 45 см3; сНу= 11,8 см3/(МПа·с); сНП = 7 см3/(МПа·с).
Параметры гидромотора: ?ГМ = 11,5 см3/рад; ?max = 314 рад/с; VГМ1 = VГМ2 = VГМ = 30 см3; сГМу= 3,1 см3/(МПа·с); сГМП = 5 см3/(МПа·с); JГМ = 0,06 кг·см2; FГM = 0.
Параметры гидролиний: l = 120 см; d0 = 2,5 см; ? = 0,2 см; EТ = 2,8 ·107 Н/см2; EЖ = 105 Н/см2.
Параметры нагрузки: JОР = 0,3·107 кг·см2; FОР= 2-104 Н·см·с,
Передаточное число редуктора i = 100.
Решение
1. Определим
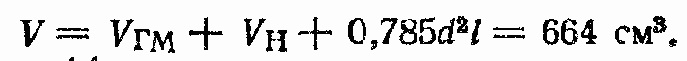
2. Вычислим коэффициент утечек
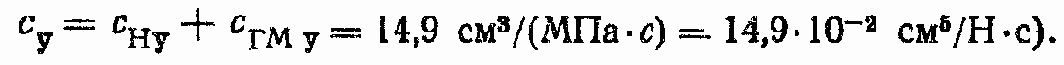
3. Рассчитаем коэффициент перетечек

4. Найдем
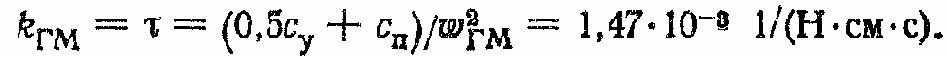
5. Определим F и J:
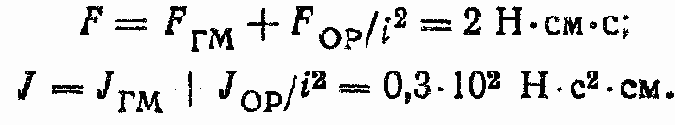
6. Рассчитаем

7. Определим
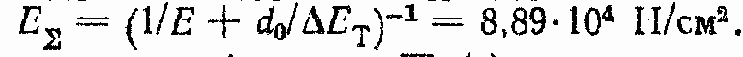
8. Найдем передаточную функцию W1(p) и ее параметры:
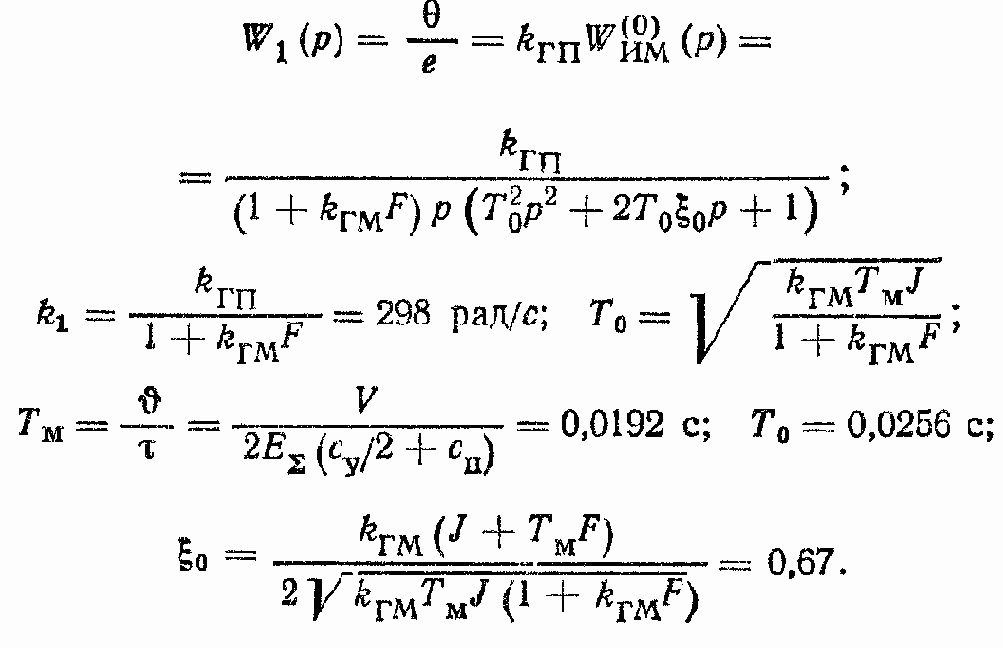
9. Вычислим передаточную функцию W2(p) и ее параметры:
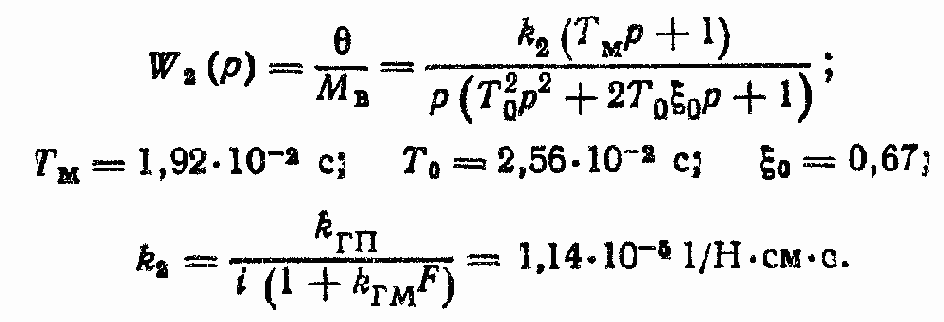
Статические характеристики ГПО (регулировочная скоростная, регулировочная моментная и механическая) обычно рассматривают при сОP = 0. Эти характеристики легко получить из уравнения (130) при p = 0:
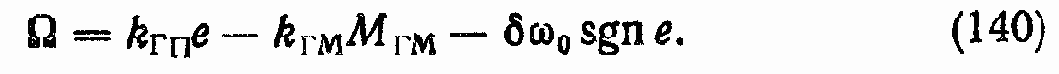
Регулировочная скоростная характеристика ? = ? (e) определяет функциональную зависимость угловой скорости вала ГМ ГПО в установившемся режиме от параметра регулирования e насоса при отсутствии нагрузки на валу ГМ (МГМ = 0).
Из уравнения (140) находим
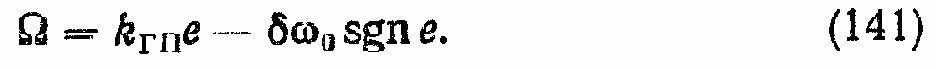
График регулировочной скоростной характеристики ГПО приведен на рис. 44, а, где

Значение ? в реальных конструкциях ГПО обычно находится в пределах 0,05 ... 0,1. Причем в начале эксплуатации эта величина имеет наименьшее значение, а затем, в процессе эксплуатации, она увеличивается.
Примечание. Уравнение (141) записано при условии, что FГM = FОР = 0. Если эти коэффициенты не равны нулю, то уравнение (141) трансформируется к виду
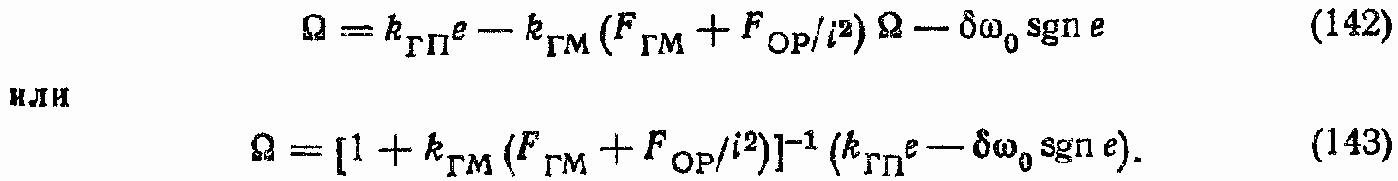
Последнее уравнение показывает, что при наличии вязкого трения в ГМ и в OP наклон скоростной характеристики уменьшается.
Регулировочная моментная характеристика МГМ = МГМ(e) определяет функциональную зависимость крутящего момента ГМ в установившемся режиме от параметра регулирования e при ? = 0 (при заторможенном вале ГМ). Уравнение регулировочной моментной характеристики получается из уравнения (140) при ? = 0:

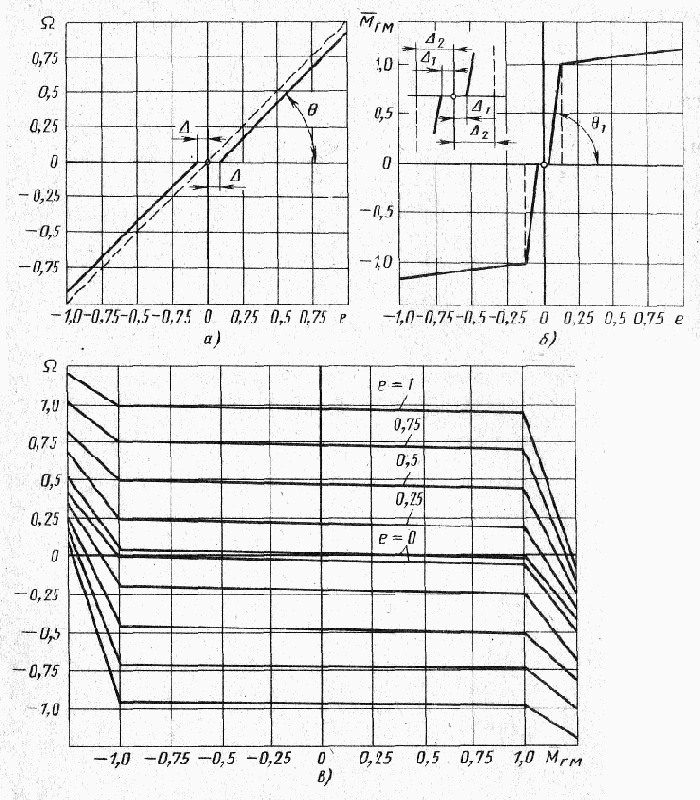
Рис. 44. Статические характеристики ГПО
где kГП = kГМ = kМ коэффициент усиления по моменту, или

При


или

где kкл — характеристика предохранительного клапана.
Регулировочная моментная характеристика ГПО изображена на рис. 44, б, где
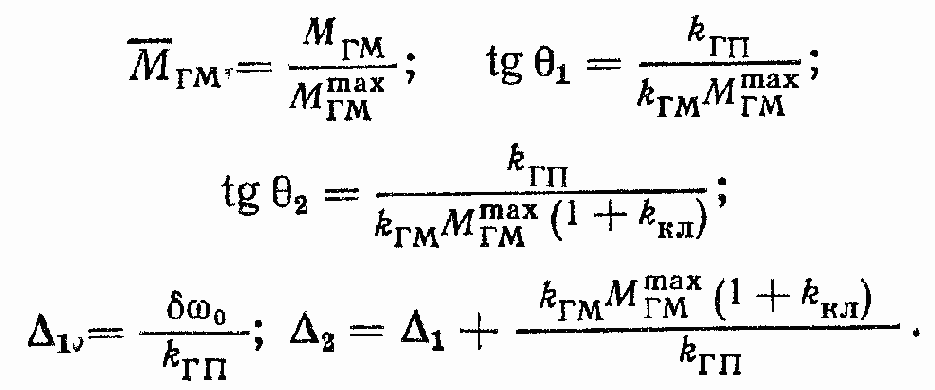
Примечание. B уравнениях (145) и (146) мы не учитывали момент трения МОРтр в OP и постоянный возмущающий момент MВ = const. Если учесть эти моменты, то уравнение (146) примет следующий вид:

Последнее уравнение показывает, что постоянный возмущающий момент и момент трения в OP увеличивают зону нечувствительности в регулировочной моментной характеристике ГПО (так же будет влиять на зону нечувствительности и момент трения МГМтр в ГМ).
Механическая характеристика ГПО определяет функциональную зависимость угловой скорости ? вала гидромотора в установившемся режиме от параметра регулирования е и от момента МГМ на валу ГМ:
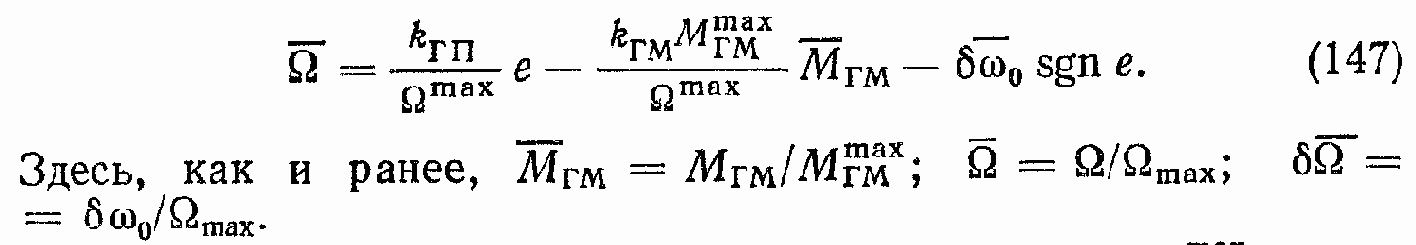
Уравнение (147) записано для случая


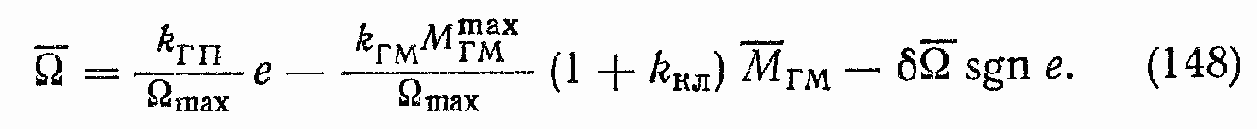
График механической характеристики ГПО представлен на рис. 44, в. Наклон характеристик
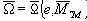
При МГМ=1 срабатывает предохранительный клапан, и наклон механической характеристики к оси абсцисс резко увеличивается (угловая скорость
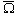
Следует отметить, что наклон механической характеристики неодинаков при различных значениях e, что объясняется нелинейной зависимостью проводимости предохранительного клапана от расхода протекающей через него РЖ «Помогающая» нагрузка (МВ = const) увеличивает
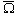
Механическая характеристика определяет весь диапазон изменения скоростей и моментов ГПО и позволяет выбрать ГПО по диаграмме нагрузки (см. п. 2 гл. 1). Как правило, ГПО выбирают так, чтобы его механическая характеристика охватывала диаграмму нагрузки с определенным запасом. Ресурс работы ГПО рассчитывают для номинальных значений скорости ???? = (0,6 ... 0,8)?max и момента
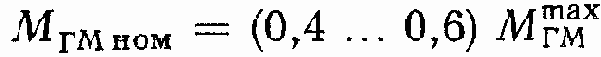
Механическая характеристика позволяет определить полезную мощность ГПО

Коэффициент полезного действия ГПО определяют с учетом потерь мощности (в ваттах) при работе системы подпитки

где QП— расход насоса системы подпитки, см3/с; ?рП — перепад давлений системы подпитки, МПа; ?П — КПД насоса системы подпитки, обычно ?П = 0,6 ... 0,9.
С учетом работы системы подпитки общий КПД ГПО находится в пределах 0,8 ... 0,9.
Зная общий КПД ГПО, по известной полезной мощности N можно определить количество выделяемой ГПО теплоты в килокалориях в час (ккал/ч):
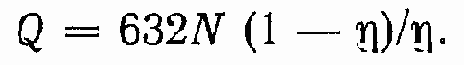
Зная Q, можно провести тепловой расчет ГПО (определить максимальную температуру ГПО)

где t0 — начальная температура (температура окружающей среды); kТП — коэффициент теплопередачи элементов конструкции ГПО, kТП = (30 ... 40) кДж/(ч·м2); FТП — площадь поверхности ГПО; Fоб — площадь поверхности теплообменника.
Назад | Содержание
| Вперед